题目内容
9.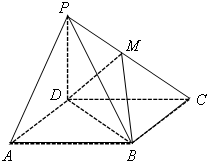 如图,四棱锥P-ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点.
如图,四棱锥P-ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点. (1)求证:AP∥平面MBD;
(2)若AD⊥PB,PD=CD,求直线MB和平面ABCD所成角的大小.
分析 (1)连结AC,交BD于点O,连结OM,证明AP∥OM,然后证明AP∥平面MBD.
(2)设H是CD的中点,连结MH,证明MH⊥平面ABCD,连结BH,说明∠MBH是直线MB和平面ABCD所成的角,然后求解∠MBH=45°,得到直线MB和平面ABCD所成角的大小.
解答 证明:(1)连结AC,交BD于点O,连结OM,
因为O,M分别是线段AC,PC的中点,
所以OM是△PAC的中位线,所以AP∥OM,
又AP?面MBD,OM?面MBD,
所以AP∥平面MBD.(5分)
解:(2)设H是CD的中点,连结MH,
因为M为PC的中点,所以MH是△PCD的中位线,
PD∥MH,
因为PD⊥平面ABCD,所以MH⊥平面ABCD,
连结BH,则BH是MB在平面ABCD内的射影,
所以∠MBH是直线MB和平面ABCD所成的角,
因为AD⊥PB,BD是PB在平面ABCD内的射影,
所以AD⊥BD,又BC∥AD,所以BC⊥BD,
所以BH=$\frac{1}{2}$CD,又MH=$\frac{1}{2}$PD,
由已知PD=CD,所以BH=MH.
所以∠MBH=45°,
即直线MB和平面ABCD所成角的大小为45°.(12分)
点评 本题考查直线与平面市场价的大小的求法,直线与平面平行的判断,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
20.经过1小时,时针旋转的角是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
4.已知点F1是抛物线C:x2=2py(p>0)的焦点,点F2为抛物线C的对称轴与其准线的交点,过F2作抛物线C的切线,切点为A,若点A恰好在以F1,F2为焦点的双曲线上,则双曲线的离心率为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$+1 | D. | $\sqrt{2}$+1 |
14.已知函数f(x)=|ln(x-1)|,若实数a,b(a<b)满足f(a)=f(b),则-a+5b的取值范围为( )
| A. | (5,8) | B. | (8,9) | C. | (5,9) | D. | (8,+∞) |
18.命题“?x∈R,cosx<$\frac{1}{2}$”的否定是( )
| A. | ?x<R,cosx≥$\frac{1}{2}$ | B. | ?x∈R,cosx>$\frac{1}{2}$ | C. | ?x<R,cosx≥$\frac{1}{2}$ | D. | ?x∈R,cosx>$\frac{1}{2}$ |
19.过点P(2,1)且在x,y轴上的截距相等的直线方程为( )
| A. | x-2y=0 | B. | 2x-y=0或x+y-3=0 | C. | x+y-3=0 | D. | x-2y=0或x+y-3=0 |