题目内容
19.设f(x)=(x2-$\frac{3}{m}$x+$\frac{5}{m^2}$)emx,其中m≠0.(1)讨论f(x)的单调性;
(2)若g(x)=f(x)-$\frac{1}{m}$x-5恰有两个零点,求m的取值范围.
分析 (1)求出f′(x),判断f′(x)的符号得出f(x)的单调性;
(2)令g(x)=0得f(x)=$\frac{1}{m}x+5$,根据f(x)与y=$\frac{1}{m}x+5$有两个交点及两函数的单调性可得f(0)<5,从而解出m的范围.
解答 解:(1)f′(x)=(2x-$\frac{3}{m}$)emx+m(x2-$\frac{3}{m}x$+$\frac{5}{{m}^{2}}$)emx=emx(mx2-x+$\frac{2}{m}$).
设h(x)=mx2-x+$\frac{2}{m}$,则△=1-8=-7<0,
∴当m>0时,h(x)>0,当m<0时,h(x)<0.
∵emx>0,
∴当m>0时,f′(x)>0,当m<0时,f′(x)<0.
∴当m>0时,f(x)为增函数,当m<0时,f(x)为减函数.
(2)令g(x)=0得f(x)=$\frac{1}{m}x+5$,
设F(x)=$\frac{1}{m}x+5$,则F(x)过点(0,5),又f(0)=$\frac{5}{{m}^{2}}$,
∵g(x)有两个零点,∴f(x)与F(x)的函数图象有两个交点,
∴$\frac{5}{{m}^{2}}<5$,解得m>1或m<-1.
点评 本题考查了函数单调性与导数的关系,函数零点与函数图象的关系,属于中档题.

练习册系列答案
相关题目
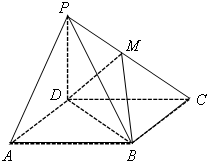 如图,四棱锥P-ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点.
如图,四棱锥P-ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点.