题目内容
18.命题“?x∈R,cosx<$\frac{1}{2}$”的否定是( )| A. | ?x<R,cosx≥$\frac{1}{2}$ | B. | ?x∈R,cosx>$\frac{1}{2}$ | C. | ?x<R,cosx≥$\frac{1}{2}$ | D. | ?x∈R,cosx>$\frac{1}{2}$ |
分析 根据命题“?x∈R,cosx<$\frac{1}{2}$”是全称命题,其否定为特称命题,即“?x∈R,cosx≥$\frac{1}{2}$”.从而得到本题答案.
解答 解:∵命题“?x∈R,cosx<$\frac{1}{2}$”是全称命题.
∴命题的否定是存在x值,使cosx<$\frac{1}{2}$不成立,
即“?x∈R,cosx≥$\frac{1}{2}$”.
故选:A
点评 本题给出全称命题,求该命题的否定形式.着重考查了含有量词的命题的否定、全称命题和特称命题等知识点,属于基础题.

练习册系列答案
相关题目
13.若f(x)=ex,则$\underset{lim}{△x→0}$$\frac{f(1+△x)-f(1)}{△x}$=( )
| A. | e | B. | -e | C. | 2e | D. | -2e |
8.用一个“+”号和一个“-”号将数字 1,2,3连成算式,不同的运算结果共有( )
| A. | 12种 | B. | 6种 | C. | 4种 | D. | 3种 |
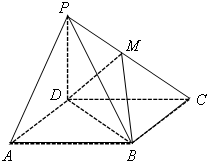 如图,四棱锥P-ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点.
如图,四棱锥P-ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点.