题目内容
14.已知函数f(x)=|ln(x-1)|,若实数a,b(a<b)满足f(a)=f(b),则-a+5b的取值范围为( )| A. | (5,8) | B. | (8,9) | C. | (5,9) | D. | (8,+∞) |
分析 根据f(x)的性质可得ln(a-1)+ln(b-1)=0,从而得出a,b的关系,从而得出得出-a+5b关于b(或者a)的函数,求出此函数的值域即可.
解答 解:f(x)=|ln(x-1)|=$\left\{\begin{array}{l}{-ln(x-1),1<x≤2}\\{ln(x-1),x>2}\end{array}\right.$,
∴f(x)在(1,2)上单调递减,在(2,+∞)上单调递增,
∵f(a)=f(b),a<b,
∴ln(a-1)+ln(b-1)=0,即ln[(a-1)(b-1)]=0,且1<a<2,b>2.
∴(a-1)(b-1)=1.
∴a=$\frac{1}{b-1}+1$=$\frac{b}{b-1}$.
∴-a+5b=$\frac{-b}{b-1}$+5b=$\frac{5{b}^{2}-6b}{b-1}$=$\frac{5(b-1)^{2}+4(b-1)-1}{b-1}$=5(b-1)-$\frac{1}{b-1}$+4,
令b-1=t,g(t)=5t-$\frac{1}{t}$+4,则g(t)在(2,+∞)上是增函数,且g(2)=8,
∴g(t)的值域为(8,+∞).
∴-a+5b的范围是(8,+∞).
故选:D.
点评 本题考查了函数的单调性与最值,对数函数的性质,属于中档题.

练习册系列答案
相关题目
5.某手机厂商推出一款6寸大屏手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如表:
女性用户:
男性用户
(Ⅰ)如果评分不低于70分,就表示该用户对手机“认可”,否则就表示“不认可”,完成下列2×2列联表,并回答是否有95%的把握认为性别和对手机的“认可”有关;
X2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{n}_{+2}}$
(Ⅱ)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意抽取3名用户,求3名用户中评分小于90分的人数的分布列和期望.
女性用户:
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 20 | 40 | 80 | 50 | 10 |
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 45 | 75 | 90 | 60 | 30 |
| 女性用户 | 男性用户 | 合计 | |
| “认可”手机 | |||
| “不认可”手机 | |||
| 合计 |
| P(X2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
(Ⅱ)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意抽取3名用户,求3名用户中评分小于90分的人数的分布列和期望.
19.空气质量指数(简称AQI)是定量描述空气质量状况的指数,其数值越大说明空气污染越严重,为了及时了解空气质量状况,广东各城市都设置了实时监测站.如表是某网站公布的广东省内21个城市在2014年12月份某时刻实时监测到的数据:
(1)请根据表中的数据,完成下列表格:
(2)统计部门从空气质量“良好”和“轻度污染”的两类城市中采用分层抽样的方式抽取6个城市,省环保部门再从中随机选取3个城市组织专家进行调研,则选取的3个城市中至少有2个城市空气质量“良好”的概率是多少?
| 城市 | AQI数值 | 城市 | AQI数值 | 城市 | AQI数值 | 城市 | AQI数值 | 城市 | AQI数值 | 城市 | AQI数值 | 城市 | AQI数值 |
| 广州 | 118 | 东莞 | 137 | 中山 | 95 | 江门 | 78 | 云浮 | 76 | 茂名 | 107 | 揭阳 | 80 |
| 深圳 | 94 | 珠海 | 95 | 湛江 | 75 | 潮州 | 94 | 河源 | 124 | 肇 庆 | 48 | 清远 | 47 |
| 佛山 | 160 | 惠州 | 113 | 汕头 | 88 | 汕尾 | 74 | 阳江 | 112 | 韶关 | 68 | 梅州 | 84 |
| 空气质量 | 优质 | 良好 | 轻度污染 | 中度污染 |
| AQI值范围 | [0,50) | [50,100) | [100,150) | [150,200) |
| 城市个数 |
4.已知F1,F2为平面内两定点,|F1F2|=6,动点M满足||MF1|-|MF2||=6,则M的轨迹是( )
| A. | 两条射线 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
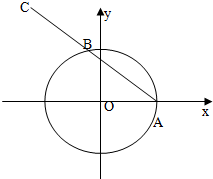 如图,已知点A(1,0),B是单位圆x2+y2=1上一动点,且点B是线段AC的中点.
如图,已知点A(1,0),B是单位圆x2+y2=1上一动点,且点B是线段AC的中点.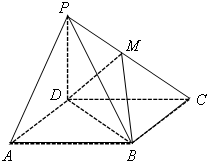 如图,四棱锥P-ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点.
如图,四棱锥P-ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点.