题目内容
17.m为何值时,关于x的方程8x2-(m-1)x+m-7=0的两根:(Ⅰ)都大于1;
(Ⅱ)一根大于2,一根小于2.
分析 (Ⅰ)设f(x)=8x2-(m-1)x+m-7,由于8x2-(m-1)x+m-7=0的两根都大于1,可得$\left\{\begin{array}{l}{f(1)>0}\\{△≥0}\\{\frac{m-1}{16}>1}\end{array}\right.$,解出即可得出.
(Ⅱ)设f(x)=8x2-(m-1)x+m-7,根据关于x的方程8x2-(m-1)x+m-7=0的两根一根大于2,一根小于2.可得f(2)<0,解出即可得出.
解答 解:(Ⅰ)设f(x)=8x2-(m-1)x+m-7,
∵8x2-(m-1)x+m-7=0的两根都大于1,
∴$\left\{\begin{array}{l}{f(1)>0}\\{△≥0}\\{\frac{m-1}{16}>1}\end{array}\right.$,
解得:m≥25.
∴m≥25时,8x2-(m-1)x+m-7=0的两根都大于1.
(Ⅱ)设f(x)=8x2-(m-1)x+m-7,
∵关于x的方程8x2-(m-1)x+m-7=0的两根一根大于2,一根小于2.
∴f(2)<0,∴32-2(m-1)+m-7<0,解得:m>27.
点评 本题考查了二次函数的单调性图象与性质、一元二次方程的根与系数的关系、一元二次不等式的解法,考查了转化能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.某手机厂商推出一款6寸大屏手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如表:
女性用户:
男性用户
(Ⅰ)如果评分不低于70分,就表示该用户对手机“认可”,否则就表示“不认可”,完成下列2×2列联表,并回答是否有95%的把握认为性别和对手机的“认可”有关;
X2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{n}_{+2}}$
(Ⅱ)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意抽取3名用户,求3名用户中评分小于90分的人数的分布列和期望.
女性用户:
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 20 | 40 | 80 | 50 | 10 |
| 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 45 | 75 | 90 | 60 | 30 |
| 女性用户 | 男性用户 | 合计 | |
| “认可”手机 | |||
| “不认可”手机 | |||
| 合计 |
| P(X2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
(Ⅱ)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意抽取3名用户,求3名用户中评分小于90分的人数的分布列和期望.
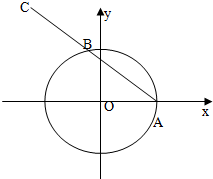 如图,已知点A(1,0),B是单位圆x2+y2=1上一动点,且点B是线段AC的中点.
如图,已知点A(1,0),B是单位圆x2+y2=1上一动点,且点B是线段AC的中点.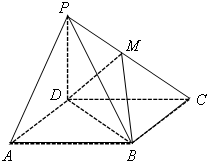 如图,四棱锥P-ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点.
如图,四棱锥P-ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点.