题目内容
4.已知点F1是抛物线C:x2=2py(p>0)的焦点,点F2为抛物线C的对称轴与其准线的交点,过F2作抛物线C的切线,切点为A,若点A恰好在以F1,F2为焦点的双曲线上,则双曲线的离心率为( )| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$+1 | D. | $\sqrt{2}$+1 |
分析 根据抛物线的性质,设出直线方程,代入抛物线方程,求得k的值,设出双曲线方程,求得2a=丨AF2丨-丨AF1丨=($\sqrt{2}$-1)p,利用双曲线的离心率公式求得e.
解答 解:直线F2A的直线方程为:y=kx-$\frac{p}{2}$,F1(0,$\frac{p}{2}$),F2(0,-$\frac{p}{2}$),
代入抛物线C:x2=2py方程,整理得:x2-2pkx+p2=0,
∴△=4k2p2-4p2=0,解得:k=±1,
∴A(p,$\frac{p}{2}$),设双曲线方程为:$\frac{{y}^{2}}{{a}^{2}}-\frac{{x}^{2}}{{b}^{2}}=1$,
丨AF1丨=p,丨AF2丨=$\sqrt{{p}^{2}+{p}^{2}}$=$\sqrt{2}$p,
2a=丨AF2丨-丨AF1丨=($\sqrt{2}$-1)p,
2c=p,
∴离心率e=$\frac{c}{a}$=$\frac{1}{\sqrt{2}-1}$=$\sqrt{2}$+1,
故答案选:D.
点评 本题考查抛物线及双曲线的方程及简单性质,考查转化思想,考查计算能力,属于中档题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
15.下列判断正确的是( )
| A. | 若x、y是实数,则x2≠y2?x≠y或x≠-y | |
| B. | 命题:“a,b都偶数,则a+b是偶数”的逆否命题是“若a+b不是偶数,则a,b都不是偶数” | |
| C. | 若“p或q”为假命题,则“非p且非q”是真命题 | |
| D. | 已知a,b,c是实数,关于x的不等式ax2+bx+c≤0的解集是空集,必有a>0且△≤0 |
16.函数f(x)=a2lnx+x2-3ax在x=1处取到极小值,则实数a的值为( )
| A. | 1 | B. | 2 | C. | 1或$\frac{1}{2}$ | D. | 1或2 |
13.若f(x)=ex,则$\underset{lim}{△x→0}$$\frac{f(1+△x)-f(1)}{△x}$=( )
| A. | e | B. | -e | C. | 2e | D. | -2e |
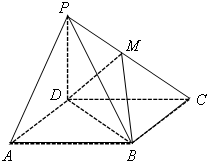 如图,四棱锥P-ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点.
如图,四棱锥P-ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点.