题目内容
1.过抛物线y2=4x的焦点作直线与其交于M、N两点,作平行四边形MONP,则点P的轨迹方程为y2=4(x-2).分析 先求出焦点的坐标,用待定系数法将MN所在的直线方程设出来,得到其参数方程,与抛物线方程联立得到M,N的横纵坐标所满足的参数方程x1+x2=$\frac{2{k}^{2}+4}{{k}^{2}}$,y1+y2=$\frac{4}{k}$,再利用平行四边形对角线交于中点的性质,求出点P(x,y),的参数方程,消参数后即可得到点P的横纵坐标所满足的方程,
解答 解:由已知抛物线y2=4x,故焦点坐标为(1,0)设M(x1,y1),N(x2,y2)
∵平行四边形MONP,
∴可设线段MN与线段OP的交点为H(x′,y′),P(x,y),
由平行四边形的性质,H是OP的中点,
∴x′=$\frac{1}{2}$x,y′=$\frac{1}{2}$y ①
当直线MN的方程为x=1时,中点就是F,此时P点的坐标为(2,0)
当直线的斜率存在在时,设斜率为k,则直线MN的方程可设为y=k(x-1)
由$\left\{\begin{array}{l}{{y}^{2}=4x}\\{y=k(x-1)}\end{array}\right.$得k2x2-2k2x+k2=4x,整理得k2x2-(2k2+4)x+k2=0,
∵M(x1,y1),N(x2,y2)
∴x1+x2=$\frac{2{k}^{2}+4}{{k}^{2}}$,
故y1+y2=k(x1-1)+k(x2-1)=k(x1+x2)-2k=k×$\frac{2{k}^{2}+4}{{k}^{2}}$)-2k=$\frac{4}{k}$
M,N的中点为H,故有x′=$\frac{{k}^{2}+2}{{k}^{2}}$,y′=$\frac{2}{k}$
又由①,可得x=$\frac{2{k}^{2}+4}{{k}^{2}}$,y=$\frac{4}{k}$
两式联立消去k得x=2+$\frac{{y}^{2}}{4}$,整理得y2=4(x-2),
验证知(2,0)在y2=4(x-2)上.
故答案为:y2=4(x-2).
点评 本题考查代入法求轨迹方程,考查直线与抛物线的位置关系,考查韦达定理的运用,考查学生分析解决问题的能力,属于中档题.

| A. | 2 | B. | -2 | C. | 3 | D. | -3 |
| A. | 1 | B. | 2 | C. | 1或$\frac{1}{2}$ | D. | 1或2 |
| A. | e | B. | -e | C. | 2e | D. | -2e |
| A. | 96 | B. | 120 | C. | 625 | D. | 1024 |
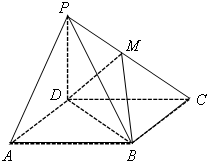 如图,四棱锥P-ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点.
如图,四棱锥P-ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点.