题目内容
8.已知命题P函数y=lg(2ax2+2x+1)的定义域为R;命题Q不等式(a-2)x2+2(a-2)x-4<0对任意实数x恒成立;若P∨Q是真命题,P∧Q是假命题;求实数a的取值范围.分析 分别求出P,Q成立的等价条件,利用P∨Q为真,P∧Q为假,确定实数a的取值范围
解答 解:若函数y=lg(2ax2+2x+1)的定义域为R,
则$\left\{\begin{array}{l}{2a>0}\\{△=4-8a<0}\end{array}\right.$,解得:a>$\frac{1}{2}$,即P:a>$\frac{1}{2}$.
若不等式(a-2)x2+2(a-2)x-4<0对任意实数x恒成立,
当a=2时,不等式等价为-4<0,成立.
当a≠0时,要使不等式恒成立,
则$\left\{\begin{array}{l}{a-2>0}\\{△={4(a-2)}^{2}+16(a-2)<0}\end{array}\right.$,
解得-2<a<2,
综上:-2<a≤2,
即Q:-2<a≤2,
若P∨Q是真命题,P∧Q是假命题,
则P,Q一真一假,
若P假Q真,则$\left\{\begin{array}{l}{a≤\frac{1}{2}}\\{-2<a≤2}\end{array}\right.$,解得-2<a≤$\frac{1}{2}$.
若P真Q假,则$\left\{\begin{array}{l}{a>\frac{1}{2}}\\{a>2或a≤-2}\end{array}\right.$,解得a>2.
综上:实数a的取值范围是(-2,$\frac{1}{2}$]∪(2,+∞).
点评 本题主要考查复合命题与简单命题之间的真假关系,先求出命题p,q成立的等价条件是解决本题的关键.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
16.已知集合$A=\{y|y=sinx,0<x<\frac{π}{2}\},B=\{x|y={log_2}x\}$,则A∩B=( )
| A. | {x|0<x<1} | B. | {x|-1<x<1} | C. | {x|-1<x<0} | D. | {x|x>0} |
3.已知P(8,a)在抛物线y2=4px上,且P到焦点的距离为10,则焦点到准线的距离为( )
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
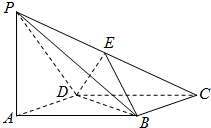 如图,四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD为菱形,E为侧棱PC上一点.
如图,四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD为菱形,E为侧棱PC上一点. 如图,有一块半径为2的半圆形纸片,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上,设CD=2x,梯形ABCD的周长为y.
如图,有一块半径为2的半圆形纸片,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上,设CD=2x,梯形ABCD的周长为y.