题目内容
3.下列结论中正确的个数是( )①若a>b,则am2>bm2;
②在线性回归分析中,相关系数r越大,变量间的相关性越强;
③已知随机变量ξ服从正态分布N(1,σ2),P(ξ≤4)=0.79,则P(ξ≤-2)=0.21;
④已知l,m为两条不同直线,α,β为两个不同平面,若α∩β=l,m∥α,m∥β,则m∥l.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由m=0,可得am2=bm2,即可判断①;
根据线性相关系数r的绝对值越接近1,两个变量的线性相关性越强,即可判断②;
由随机变量ξ服从正态分布N(1,σ2),则曲线关于x=1对称,即可判断③;
运用线面平行的判定定理和性质定理,即可判断④.
解答 解:对于①,若a>b,且m=0,则am2=bm2,若m≠0,则am2>bm2,故①错误;
对于②,根据线性相关系数r的绝对值越接近1,两个变量的线性相关性越强;反之,线性相关性越弱,判断②错误;
对于③,已知随机变量ξ服从正态分布N(1,σ2),P(ξ≤4)=0.79,则曲线关于x=1对称,可得P(ξ>4)=1-0.79=0.21,P(ξ≤-2)=P(ξ>4)=0.21,故③正确;
对于④,已知l,m为两条不同直线,α,β为两个不同平面,若α∩β=l,m∥α,
过m的一个平面与α交于a,由线面平行的性质定理可得,m∥a,同理由m∥β,过m的平面与β交于b,可得
m∥b,则a∥b,a?β,可得a∥β,再由线面平行的性质定理可得a∥l,则m∥l,故④正确.
其中正确的个数为2.
故选:B.
点评 本题考查命题的真假判断和应用,考查不等式的性质和线性相关的强度,以及正态分布的特点和空间线面平行的判定和性质,考查推理能力和判断能力,属于中档题.

练习册系列答案
相关题目
13.下列命题中的假命题是( )
| A. | log23<log35 | B. | ?x∈(-∞,0),ex>x+1 | ||
| C. | ${log_{\frac{1}{2}}}3<{(\frac{1}{2})^3}<{3^{\frac{1}{2}}}$ | D. | ?x>0,x>sinx |
11.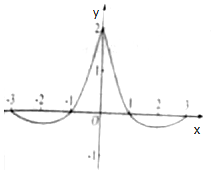 已知函数f(x)=$\frac{{cos({ωx+φ})}}{{a•{e^{|x|}}}}$(ω>0,|φ|<$\frac{π}{2}$,a∈R)在区间[-3,3]上的图象如图所示,则$\frac{ω}{a}$可取( )
已知函数f(x)=$\frac{{cos({ωx+φ})}}{{a•{e^{|x|}}}}$(ω>0,|φ|<$\frac{π}{2}$,a∈R)在区间[-3,3]上的图象如图所示,则$\frac{ω}{a}$可取( )
 已知函数f(x)=$\frac{{cos({ωx+φ})}}{{a•{e^{|x|}}}}$(ω>0,|φ|<$\frac{π}{2}$,a∈R)在区间[-3,3]上的图象如图所示,则$\frac{ω}{a}$可取( )
已知函数f(x)=$\frac{{cos({ωx+φ})}}{{a•{e^{|x|}}}}$(ω>0,|φ|<$\frac{π}{2}$,a∈R)在区间[-3,3]上的图象如图所示,则$\frac{ω}{a}$可取( )| A. | 4π | B. | 2π | C. | π | D. | $\frac{π}{2}$ |
8.在等差数列{an}中,若a1=6,a3=2,则a5=( )
| A. | 6 | B. | 4 | C. | 0 | D. | -2 |