题目内容
18.等差数列{an}中,已知a3=5,且a1,a2,a3为递增的等比数列.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}的通项公式${b_n}=\left\{\begin{array}{l}{a_{\frac{n+1}{2}}},n=2k-1\\{2^{\frac{n}{2}-1}},n=2k\end{array}\right.$(k∈N*),求数列{bn}的前n项和Sn.
分析 (Ⅰ)设数列{an}的公差为d,由题意$({{a_3}-2d})({{a_3}+2d})={({{a_3}-d})^2}$,a3=5,单人化简解出即可得出.
(Ⅱ)对n分类讨论,分组求和即可得出.
解答 解:(Ⅰ)设数列{an}的公差为d,由题意$({{a_3}-2d})({{a_3}+2d})={({{a_3}-d})^2}$,a3=5.
即d2-2d=0,解之得d=2,或d=0(舍去),
所以an=a3+(n-3)d=2n-1,即an=2n-1,n∈N*为所求.
(Ⅱ)当n=2k,k∈N*时,
Sn=b1+b2+…+bn=b1+b3+…+b2k-1+b2+b4+…+b2k=a1+a2+…+ak+(20+21+…+2k-1)
=$\frac{{k({1+2k-1})}}{2}+\frac{{1-{2^k}}}{1-2}$=k2+2k-1=$\frac{n^2}{4}+{2^{\frac{n}{2}}}-1$;
当n=2k-1,k∈N*时,n+1=2k,Sn=Sn+1-bn+1=$\frac{{{{({n+1})}^2}}}{4}+{2^{\frac{n+1}{2}}}-1-{2^{\frac{n+1}{2}-1}}$=$\frac{{{n^2}+2n-3}}{4}+{2^{\frac{n-1}{2}}}$.
综上,${S_n}=\left\{\begin{array}{l}\frac{n^2}{4}+{2^{\frac{n}{2}}}-1,n=2k\\ \frac{{{n^2}+2n-3}}{4}+{2^{\frac{n-1}{2}}},n=2k-1\end{array}\right.$(k∈N*).
点评 本题考查了等差数列与等比数列的通项公式与求和公式、分类讨论方法,考查了推理能力与计算能力,属于中档题.

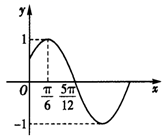
| A. | $f(x)=sin({2x-\frac{π}{6}})$(x∈R) | B. | $f(x)=sin({2x+\frac{π}{6}})$(x∈R) | C. | $f(x)=sin({2x-\frac{π}{3}})$(x∈R) | D. | $f(x)=sin({2x+\frac{π}{3}})$(x∈R) |
| A. | y=±$\frac{1}{2}$x | B. | y=±$\sqrt{3}$x | C. | y=±2x | D. | y=±$\frac{{\sqrt{3}}}{3}$x |
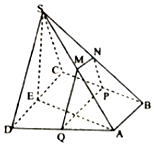 如图,四棱锥S-ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=CD=SD=AD=2AB=2,M,N分别为SA,SB的中点,E为CD的中点,过M,N作平面MNPQ分别与交BC,AD于点P,Q.
如图,四棱锥S-ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=CD=SD=AD=2AB=2,M,N分别为SA,SB的中点,E为CD的中点,过M,N作平面MNPQ分别与交BC,AD于点P,Q.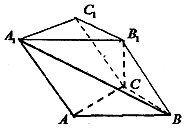 如图,斜三棱柱ABC-A1B1C1中,侧面AA1B1B为菱形,底面△ABC是等腰直角三角形,∠BAC=90°,A1B⊥B1C.
如图,斜三棱柱ABC-A1B1C1中,侧面AA1B1B为菱形,底面△ABC是等腰直角三角形,∠BAC=90°,A1B⊥B1C.