题目内容
函数y=|1-x|+
的定义域为（ ）
| x |
| A、{x|x≤1} |
| B、{x|x≥o} |
| C、{x|x≥1或x≤0} |
| D、{x|0≤x≤1} |
考点：函数的定义域及其求法
专题：
分析：结合二次根式的性质，从而得出答案．
解答：
解：由题意得：x≥0，
∴函数的定义域是：{x}x≥0}，
故选：B．
∴函数的定义域是：{x}x≥0}，
故选：B．
点评：本题考查了函数的定义域问题，是一道基础题．
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
已知：命题p：“a＜b”是“am2＜bm2”的充要条件”；命题q：“?x0∈R，x02+x0-2＞0”．则下列命题正确的是（ ）
| A、命题“p∧q”是真命题 |
| B、命题“p∧（￢q）”是真命题 |
| C、命题“（￢p）∧q”是真命题 |
| D、命题“（￢p）∧（￢q）”是真命题 |
在数列{an}中，a1=3，an=2an-1+n-2（n≥2，且n∈N*），下列哪一个是数列中的项（ ）
| A、210-10 |
| B、211-10 |
| C、212-10 |
| D、213-10 |
（文）如图，在正方体ABCD-A1B1C1D1中，CC1与平面A1BD所成的角为α，则cosα的值是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
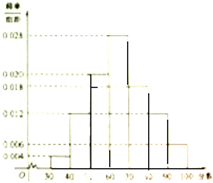某校高一年级共有800名学生，其中男生480名，女生320名，在某次满分为100分的数学考试中，所有学生成绩在30分及30分以上，成绩在“80分及80分以上”的学生视为优秀．现按性别采用分层抽样的方法共抽取100名学生，将他们的成绩按[30，40]、[40，50]、[50，60]、[60，70]、[70，80]、[80，90]、[90，100]分成七组．得到的频率分布直方图如图所示：