题目内容
已知向量
=(cos(x-
),0),
=(2,0),x∈R,函数f(x)=
•
.
(1)求函数f(x)的表达式;
(2)求f(π)的值;
(3)若f(α+
)=
,α∈(-
,0),求f(2α)的值.
| m |
| π |
| 6 |
| n |
| m |
| n |
(1)求函数f(x)的表达式;
(2)求f(π)的值;
(3)若f(α+
| 2π |
| 3 |
| 6 |
| 5 |
| π |
| 2 |
考点:三角函数中的恒等变换应用,平面向量数量积的坐标表示、模、夹角
专题:综合题,三角函数的求值,平面向量及应用
分析:(1)利用向量是数量积公式,可得函数f(x)的表达式;
(2)代入函数f(x)的表达式,可求f(π)的值;
(3)由f(α+
)=
,α∈(-
,0),求出sinα=-
,cosα,再利用角的变换,即可求f(2α)的值.
(2)代入函数f(x)的表达式,可求f(π)的值;
(3)由f(α+
| 2π |
| 3 |
| 6 |
| 5 |
| π |
| 2 |
| 3 |
| 5 |
解答:
解:(1)∵
=(cos(x-
),0),
=(2,0),x∈R,
∴f(x)=
•
=2cos(x-
),即函数f(x)=2cos(x-
).(3分)
(2)f(π)=2cos(π-
)=-2cos
=-
(6分)
(3)∵f(α+
)=2cos(α+
-
)=2cos(α+
)=-2sinα,
又f(α+
)=
,∴-2sinα=
,即sinα=-
.(7分)
∵α∈(-
,0),∴cosα=
=
=
.(8分)
∴sin2α=2sinαcosα=2×(-
)×
=-
,(9分)
cos2α=2cos2α-1=2×(
)2-1=
.(10分)
∴f(2α)=2cos(2α-
)=2cos2αcos
+2sin2αsin
(11分)
=2×
×
+2×(-
)×
=
.(12分)
| m |
| π |
| 6 |
| n |
∴f(x)=
| m |
| n |
| π |
| 6 |
| π |
| 6 |
(2)f(π)=2cos(π-
| π |
| 6 |
| π |
| 6 |
| 3 |
(3)∵f(α+
| 2π |
| 3 |
| 2π |
| 3 |
| π |
| 6 |
| π |
| 2 |
又f(α+
| 2π |
| 3 |
| 6 |
| 5 |
| 6 |
| 5 |
| 3 |
| 5 |
∵α∈(-
| π |
| 2 |
| 1-sin2α |
1-(-
|
| 4 |
| 5 |
∴sin2α=2sinαcosα=2×(-
| 3 |
| 5 |
| 4 |
| 5 |
| 24 |
| 25 |
cos2α=2cos2α-1=2×(
| 4 |
| 5 |
| 7 |
| 25 |
∴f(2α)=2cos(2α-
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
=2×
| 7 |
| 25 |
| ||
| 2 |
| 24 |
| 25 |
| 1 |
| 2 |
7
| ||
| 25 |
点评:本题考查向量知识的运用,考查同角三角函数关系,考查角的变换,考查小时分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=
,则f(2014)的值为( )
|
A、
| ||
| B、2 | ||
C、-
| ||
| D、-2 |
设函数f(x)=(x-1)kcosx(k∈N*),则( )
| A、当k=2013时,f(x)在x=1处取得极小值 |
| B、当k=2013时,f(x)在x=1处取得极大值 |
| C、当k=2014时,f(x)在x=1处取得极小值 |
| D、当k=2014时,f(x)在x=1处取得极大值 |
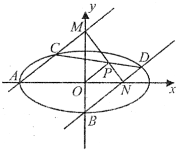 如图,过椭圆L的左顶点A(-3,0)和下顶点B且斜率均为k的两直线l1,l2分别交椭圆于C,D,又l1交y轴于M,l2交x轴于N,且CD与MN相交于点P,当k=3时,△ABM是直角三角形.
如图,过椭圆L的左顶点A(-3,0)和下顶点B且斜率均为k的两直线l1,l2分别交椭圆于C,D,又l1交y轴于M,l2交x轴于N,且CD与MN相交于点P,当k=3时,△ABM是直角三角形.