题目内容
袋中装有黑球和白球共7个,从中任取2个球都是黑球的概率为
,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取…,取球后不放回,直到两人中有一人取到白球时终止,每个球在每一次被取出的机会是等可能的,用ξ表示取球终止所需要的取球次数.
(Ⅰ)求随机变量ξ的分布列及数学期望;
(Ⅱ)求乙取到白球的概率.
| 2 |
| 7 |
(Ⅰ)求随机变量ξ的分布列及数学期望;
(Ⅱ)求乙取到白球的概率.
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式
专题:概率与统计
分析:(Ⅰ)设袋中原有n个黑球,由题意知
=
,求出黑球有4个,白球有3个.由题意,ξ的可能取值为1,2,3,4,5,分别求出其概率,由此能求出ξ的分布列及数学期望.
(Ⅱ)由乙后取,知乙只有可能在第二次,第四次取球,由此能求出乙取到白球的概率.
| 1 |
| 7 |
| ||
|
(Ⅱ)由乙后取,知乙只有可能在第二次,第四次取球,由此能求出乙取到白球的概率.
解答:
解:(Ⅰ)设袋中原有n个黑球,
由题意知
=
…(1分)
=
=
,
解得n=4或n=-3(舍去) …(3分)
∴黑球有4个,白球有3个.
由题意,ξ的可能取值为1,2,3,4,5…(4分)
P(ξ=1)=
;P(ξ=2)=
=
,
P(ξ=3)=
=
,
P(ξ=4)=
=
,
P(ξ=5)=
=
…(7分)(错一个扣一分,最多扣3分)
∴ξ的分布列为
…(8分)
所以数学期望为:Eξ=
+2×
+3×
+4×
+5×
=2…(9分)
(Ⅱ)∵乙后取,
∴乙只有可能在第二次,第四次取球,
记乙取到白球为事件A,
则P(A)=P(ξ=2)+P(ξ=4)=
+
=
,…(11分)
答:乙取到白球的概率为
.…(12分)
由题意知
| 1 |
| 7 |
| ||
|
=
| ||
|
| n(n-1) |
| 7×6 |
解得n=4或n=-3(舍去) …(3分)
∴黑球有4个,白球有3个.
由题意,ξ的可能取值为1,2,3,4,5…(4分)
P(ξ=1)=
| 3 |
| 7 |
| 4×3 |
| 7×6 |
| 2 |
| 7 |
P(ξ=3)=
| 4×3×3 |
| 7×6×5 |
| 6 |
| 35 |
P(ξ=4)=
| 4×3×2×3 |
| 7×6×5×4 |
| 3 |
| 35 |
P(ξ=5)=
| 4×3×2×1×3 |
| 7×6×5×4×3 |
| 1 |
| 35 |
∴ξ的分布列为
| ξ | 1 | 2 | 3 | 4 | 5 | ||||||||||
| P |
|
|
|
|
|
所以数学期望为:Eξ=
| 3 |
| 7 |
| 2 |
| 7 |
| 6 |
| 35 |
| 3 |
| 35 |
| 1 |
| 35 |
(Ⅱ)∵乙后取,
∴乙只有可能在第二次,第四次取球,
记乙取到白球为事件A,
则P(A)=P(ξ=2)+P(ξ=4)=
| 2 |
| 7 |
| 3 |
| 35 |
| 13 |
| 35 |
答:乙取到白球的概率为
| 13 |
| 35 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,在历年高考中都是必考题型.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )


| A、48cm3 |
| B、98cm3 |
| C、98cm3 |
| D、78cm3 |
已知函数f(x)=
,则f(2014)的值为( )
|
A、
| ||
| B、2 | ||
C、-
| ||
| D、-2 |
 如图,设椭圆C:
如图,设椭圆C: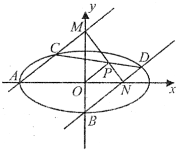 如图,过椭圆L的左顶点A(-3,0)和下顶点B且斜率均为k的两直线l1,l2分别交椭圆于C,D,又l1交y轴于M,l2交x轴于N,且CD与MN相交于点P,当k=3时,△ABM是直角三角形.
如图,过椭圆L的左顶点A(-3,0)和下顶点B且斜率均为k的两直线l1,l2分别交椭圆于C,D,又l1交y轴于M,l2交x轴于N,且CD与MN相交于点P,当k=3时,△ABM是直角三角形.