题目内容
已知等差数列{an}中,sn表示前n项和,a2+a5=13,S5=25.求:
(Ⅰ) 首项a1和公差d;
(Ⅱ) 该数列的前20项的和S20的值.
(Ⅰ) 首项a1和公差d;
(Ⅱ) 该数列的前20项的和S20的值.
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:(Ⅰ)直接利用等差数列的通项公式与前n项和公式结合已知列方程组求得首项a1和公差d;
(Ⅱ)直接利用等差数列的前n项和得答案.
(Ⅱ)直接利用等差数列的前n项和得答案.
解答:
解:(Ⅰ) 由等差数列{an}的通项公式:an=a1+(n-1)d及前n项和公式:Sn=na1+
,
得
,
即
,
解得a1=-1,d=3;
(Ⅱ) 由等差数列{an}的前n项和公式:Sn=na1+
,
得S20=20×(-1)+
=550.
| n(n-1)d |
| 2 |
得
|
即
|
解得a1=-1,d=3;
(Ⅱ) 由等差数列{an}的前n项和公式:Sn=na1+
| n(n-1)d |
| 2 |
得S20=20×(-1)+
| 20×19×3 |
| 2 |
点评:本题考查了等差数列的通项公式,考查了等差数列的前n项和,是基础的计算题.

练习册系列答案
相关题目
设点A(2,-3),B(-3,-2),直线l过原点且与线段AB相交,则l的斜率k的取值范围是( )
A、k≥
| ||||
B、k≥
| ||||
C、-
| ||||
D、-
|
设定义在R上的偶函数f(x)满足f(1-x)=f(x+1),且当x∈[0,1]时,f(x)=x3,若方程f(x)-cos
x-a=0(a<0)无解,则实数a的取值范围是( )
| π |
| 2 |
| A、(-∞,-2) |
| B、(-∞,-2] |
| C、(-∞,-1] |
| D、(-∞,-1) |
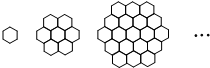 蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.则f(10)=
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.则f(10)=