题目内容
在{an}为等比数列,a1=12,a2=24,则a3= .
考点:等比数列的通项公式
专题:等差数列与等比数列
分析:利用等比数列的通项公式求解.
解答:
解:∵在{an}为等比数列,a1=12,a2=24,
∴q=
=2,
∴a3=24×2=48.
故答案为:48.
∴q=
| 24 |
| 12 |
∴a3=24×2=48.
故答案为:48.
点评:本题考查等比数列的第3项的求法,是基础题,解题时要认真审题,注意等比数列的通项公式的应用.

练习册系列答案
相关题目
在△ABC中,a、b、c分别是∠A、∠B、∠C的对边,若C=60°,3a=2c=6,则b值为( )
A、
| ||
B、
| ||
C、
| ||
D、1+
|
函数y=2sin(
-x),x∈[
,
]的最小值和最大值分别是( )
| π |
| 3 |
| π |
| 6 |
| 2π |
| 3 |
A、-
| ||
| B、-1和2 | ||
| C、1和3 | ||
| D、1和2 |
函数y=
的图象大致是( )
| x2 |
| 2x-1 |
A、 |
B、 |
C、 |
D、 |
 如图,DC⊥平面ABC,∠BAC=90°,AC=
如图,DC⊥平面ABC,∠BAC=90°,AC=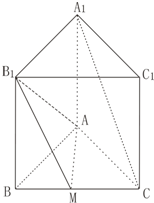 如图正三棱柱ABC-A1B1C1中底面边长AB=1,高BB1=1,M为底面BC边的中点.
如图正三棱柱ABC-A1B1C1中底面边长AB=1,高BB1=1,M为底面BC边的中点.