题目内容
在右侧的表格中，各数均为正数，且每行中的各数从左到右成等差数列，每列中的各数从上到下成等比数列，那么x+y+z= ．
| 2 | x | 3 | ||||
| y | a |
| ||||
|
| z |
考点：等比数列的性质
专题：计算题,等差数列与等比数列
分析：先利用每一纵列成等比数列，所以由第一列，可得y=1，再利用每一横行成等差数列，所以由第二行可得a=
，由第三行可得z=
，进而求出x，即可求出x+y+z．
| 5 |
| 4 |
| 3 |
| 4 |
解答：
解：因为每一纵列成等比数列，所以由第一列，可得y=1，
又因为每一横行成等差数列，所以由第二行可得a=
，由第三行可得z=
由第一列，可得x=
，
所以x+y+z=
．
故答案为：
．
又因为每一横行成等差数列，所以由第二行可得a=
| 5 |
| 4 |
| 3 |
| 4 |
由第一列，可得x=
| 5 |
| 2 |
所以x+y+z=
| 17 |
| 4 |
故答案为：
| 17 |
| 4 |
点评：本小题主要考查等差数列、等比数列等基础知识，考查运算求解能力．
练习册系列答案
阅读快车系列答案
相关题目
已知向量
=（2，8），
=（-4，2）．若
=2
-
，则向量
=（ ）
| a |
| b |
| c |
| a |
| b |
| c |
| A、（0，18） |
| B、（8，14） |
| C、（12，12） |
| D、（-4，20） |
已知圆C经过点A（1，1）和点B（2，-2），且圆心C在直线x-y+1=0上，则圆心C的坐标是（ ）
| A、（-4，-3） |
| B、（-3，-2） |
| C、（4，5） |
| D、（3，4） |
如图，O为坐标原点，点A，B在⊙O上，且点A在第一象限，点B（-已知数列{an}为等差数列，且a3=7，a7=3，则a10等于（ ）
| A、0 | B、1 | C、9 | D、10 |
设函数f（x）=3x+bcosx，x∈R，则“b=0”是“函数f（x）为奇函数”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知集合M={x|x2-2x-3＞0}，N={x|-1≤x≤1}，则M∩（∁RN）=（ ）
| A、（-∞，-3）∪（1，3） |
| B、（-∞，-1）∪（1，+∞） |
| C、（-∞，-1）∪（3，+∞） |
| D、（-∞，-3）∪（1，+∞） |
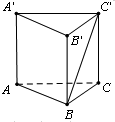如图所示，在底面为正三角形的三棱柱ABC-A1B1C1中，若AA1⊥平面ABC，AB=| 2 |
| A、60° | B、45° |
| C、90° | D、120° |