题目内容
已知数列{an}满足a1=0,a2=2,且对任意m、n∈N*都有a2m-1+a2n-1=2am+n-1+2(m-n)2
(1)求a3,a5;
(2)设cn=(an+1-an) qn-1(q≠0,n∈N*),求数列{cn}的前n项和Sn.
(1)求a3,a5;
(2)设cn=(an+1-an) qn-1(q≠0,n∈N*),求数列{cn}的前n项和Sn.
考点:数列递推式,数列的求和
专题:等差数列与等比数列
分析:(1)利用赋值法求出数列中的各个项.
(2)首先求出新构造数列的通项公式,进一步利用分裂讨论的方法求出数列的前n项和.
(2)首先求出新构造数列的通项公式,进一步利用分裂讨论的方法求出数列的前n项和.
解答:
解:(1)由题意,令m=2,n=1,可得a3=2a2-a1+2=6
再令m=3,n=1,可得a5=2a3-a1+8=20
(2)由已知:令m=1,可得
an=
-(n-1)2.
令m=2,可得
an+1=
-(2-n)2.
那么an+1-an=
+(n-1)2-(2-n)2
=
+2n-3
=2n
于是cn=2nqn-1.
当q=1时,Sn=2+4+6+…+2n=n(n+1)
当q≠1时,Sn=2•q0+4•q1+6•q2+…+2n•qn-1.
两边同乘以q,可得
qSn=2•q1+4•q2+6•q3+…+2n•qn.
上述两式相减得
(1-q)Sn=2(1+q+q2+…+qn-1)-2nqn
=2•
-2nqn
=2•
所以Sn=2•
综上所述,Sn=
再令m=3,n=1,可得a5=2a3-a1+8=20
(2)由已知:令m=1,可得
an=
| a2n-1+a1 |
| 2 |
令m=2,可得
an+1=
| a2n-1+a3 |
| 2 |
那么an+1-an=
| a3-a1 |
| 2 |
=
| 6-0 |
| 2 |
=2n
于是cn=2nqn-1.
当q=1时,Sn=2+4+6+…+2n=n(n+1)
当q≠1时,Sn=2•q0+4•q1+6•q2+…+2n•qn-1.
两边同乘以q,可得
qSn=2•q1+4•q2+6•q3+…+2n•qn.
上述两式相减得
(1-q)Sn=2(1+q+q2+…+qn-1)-2nqn
=2•
| 1-qn |
| 1-q |
=2•
| 1-(n+1)qn+nqn+1 |
| 1-q |
所以Sn=2•
| nqn+1-(n+1)qn+1 |
| (q-1)2 |
综上所述,Sn=
|
点评:本题考查的知识要点:利用数列的通项公式求出数列中的各个项,根据构造的新数列,利用分类法求数列的和,属于中等题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知数列{an}为等差数列,且a3=7,a7=3,则a10等于( )
| A、0 | B、1 | C、9 | D、10 |
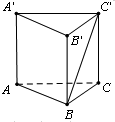 如图所示,在底面为正三角形的三棱柱ABC-A1B1C1中,若AA1⊥平面ABC,AB=
如图所示,在底面为正三角形的三棱柱ABC-A1B1C1中,若AA1⊥平面ABC,AB=| 2 |
| A、60° | B、45° |
| C、90° | D、120° |
三次函数f(x)=x3+bx2+cx+d(b,c,d∈R)在区间[-1,2]上是减函数,那么b+c的取值范围是( )
A、(-∞,
| ||
B、(-∞, -
| ||
| C、A(x0,f(x0)) | ||
D、(-∞,-
|
已知函数y=f(x)满足f(π-x)=f(x),且当x∈(-
,
)时,f(x)=xsinx-cosx,则( )
| π |
| 2 |
| π |
| 2 |
| A、f(2)<f(3)<f(4) |
| B、f(3)<f(4)<f(2) |
| C、f(4)<f(3)<f(2) |
| D、f(4)<f(2)<f(3) |
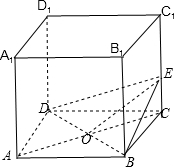 如图,正方体ABCD-A1B1C1D1,边长为1,E为CC1上一点,且EC=
如图,正方体ABCD-A1B1C1D1,边长为1,E为CC1上一点,且EC=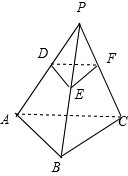 如图,已知点P为△ABC所在平面外任一点点D、E、F分别在射线PA、PB、PC上并且
如图,已知点P为△ABC所在平面外任一点点D、E、F分别在射线PA、PB、PC上并且