题目内容
不等式4x2-4x-15≥0的解集是 .
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:根据二次不等式对应的方程有两不等实根,且对应的二次函数开口向上,借助于三个二次可求不等式的解集.
解答:
解:不等式4x2-4x-15≥0对应二次方程4x2-4x-15=0的两根为x1=-
,x2=
,
对应的二次函数y=4x2-4x-15开口向上,所以4x2-4x-15≥0的解集为(-∞,-
]∪[
,+∞).
故答案为:(-∞,-
]∪[
,+∞).
| 3 |
| 2 |
| 5 |
| 2 |
对应的二次函数y=4x2-4x-15开口向上,所以4x2-4x-15≥0的解集为(-∞,-
| 3 |
| 2 |
| 5 |
| 2 |
故答案为:(-∞,-
| 3 |
| 2 |
| 5 |
| 2 |
点评:本题考查了一元二次不等式的解法,考查了三个二次之间的关系,是综合题.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
已知集合M={x|x2-2x-3>0},N={x|-1≤x≤1},则M∩(∁RN)=( )
| A、(-∞,-3)∪(1,3) |
| B、(-∞,-1)∪(1,+∞) |
| C、(-∞,-1)∪(3,+∞) |
| D、(-∞,-3)∪(1,+∞) |
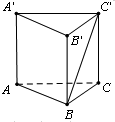 如图所示,在底面为正三角形的三棱柱ABC-A1B1C1中,若AA1⊥平面ABC,AB=
如图所示,在底面为正三角形的三棱柱ABC-A1B1C1中,若AA1⊥平面ABC,AB=| 2 |
| A、60° | B、45° |
| C、90° | D、120° |
已知函数y=f(x)满足f(π-x)=f(x),且当x∈(-
,
)时,f(x)=xsinx-cosx,则( )
| π |
| 2 |
| π |
| 2 |
| A、f(2)<f(3)<f(4) |
| B、f(3)<f(4)<f(2) |
| C、f(4)<f(3)<f(2) |
| D、f(4)<f(2)<f(3) |
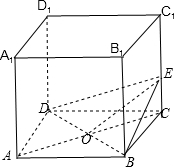 如图,正方体ABCD-A1B1C1D1,边长为1,E为CC1上一点,且EC=
如图,正方体ABCD-A1B1C1D1,边长为1,E为CC1上一点,且EC=