题目内容
11.已知数列{an}的前n项和为Sn,且an=2-2Sn(n∈N*).(1)求数列{an}的通项公式;
(2)设数列{bn}满足bn=log3(1-Sn)(n∈N*),若$\frac{1}{{{b_2}{b_3}}}+\frac{1}{{{b_3}{b_4}}}+…+\frac{1}{{{b_n}{b_{n+1}}}}=\frac{25}{51}$,求自然数n的值.
分析 (1)根据an=Sn-Sn-1得出递推公式,得出{an}为等比数列,再计算a1,得出通项公式;
(2)计算bn,利用裂项法求和,根据求和公式列方程得出n.
解答 解:(1)由an=2-2Sn得2Sn=2-an,
∴2Sn-1=2-an-1,(n≥2)
当n=1时,a1=$\frac{2}{3}$,
当n≥2时,2an=an-1-an,即an=$\frac{1}{3}$an-1,
∴{an}是以$\frac{2}{3}$为首项,以$\frac{1}{3}$为公比的等比数列,
∴an=$\frac{2}{3}$×($\frac{1}{3}$)n-1=$\frac{2}{{3}^{n}}$.
(2)Sn=$\frac{\frac{2}{3}(1-\frac{1}{{3}^{n}})}{1-\frac{1}{3}}$=1-$\frac{1}{{3}^{n}}$,∴bn=log3$\frac{1}{{3}^{n}}$=-n,∴$\frac{1}{{b}_{n}{b}_{n+1}}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$,
∴$\frac{1}{{b}_{2}{b}_{3}}$+$\frac{1}{{b}_{3}{b}_{4}}$+…+$\frac{1}{{b}_{n}{b}_{n+1}}$=$\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}$+…+$\frac{1}{n}-\frac{1}{n+1}$=$\frac{1}{2}-$$\frac{1}{n+1}$,
∴$\frac{1}{2}-$$\frac{1}{n+1}$=$\frac{25}{51}$,解得n=101.
点评 本题考查了等比数列的判断,裂项法求和,属于基础题.

 阅读快车系列答案
阅读快车系列答案| 分数 | [0,90) | [90,105) | [105,1200) | [120,135) | [135,150) |
| 甲班频数 | 5 | 6 | 4 | 4 | 1 |
| 乙班频数 | 1 | 3 | 6 | 5 |
(2)现从上述40人中,学校按成绩是否优良采用分层抽样的方法抽取8人进行考核,在这8人中,记成绩不优良的乙班人数为X,求X的分布列和数学期望.
| 甲班 | 乙班 | 总计 | |
| 成绩优良 | |||
| 成绩不优良 | |||
| 总计 |
临界值表:
| P(K2≥k0) | 0.10 | 0.050 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | $2\sqrt{3}$ | B. | 4 | C. | $4\sqrt{3}$ | D. | 8 |
| A. | 若α∩β=a,β∩γ=b,a∥b,则α∥γ | B. | 若a∥α,a∥β,b∥α,b∥β,则α∥β | ||
| C. | 若α⊥β,α∩β=a,b?β,a⊥b,则b⊥α | D. | 若a?α,b?α,l⊥α,l⊥b,则l⊥α |
 如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,四边形ABCD是梯形,∠ABC=90°,BC∥AD,且$PA=AB=BC=\frac{1}{2}AD=1$.
如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,四边形ABCD是梯形,∠ABC=90°,BC∥AD,且$PA=AB=BC=\frac{1}{2}AD=1$.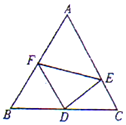 如图,在边长为2的正三角形△ABC中,D为BC的中点,E,F分别在边CA,AB上.
如图,在边长为2的正三角形△ABC中,D为BC的中点,E,F分别在边CA,AB上.