题目内容
已知不同的三点A、B、C满足
=λ
(λ∈R,λ≠0),使得关于x的方程x2
+x
-
=
有解(点O不在直线AB上),则此方程在实数范围内的解集为( )
| AB |
| BC |
| OA |
| OB |
| OC |
| 0 |
| A、∅ | ||||||||
| B、{-1,0} | ||||||||
| C、{-1} | ||||||||
D、{
|
考点:向量在几何中的应用
专题:平面向量及应用
分析:将
=λ
中的
,
用向量
,
,
表示,于是
可用
,
表示,而方程x2
+x
-
=
可改写成
=x2
+x
,根据平面向量基本定理,存在唯一的实数对λ1,λ2,使得
=λ1
+λ2
,从而得到关于x的一元二次方程,探究此方程即可得解集.
| AB |
| BC |
| AB |
| BC |
| OA |
| OB |
| OC |
| OC |
| OA |
| OB |
| OA |
| OB |
| OC |
| 0 |
| OC |
| OA |
| OB |
| OC |
| OA |
| OB |
解答:
解:由
=λ
,得
-
=λ(
-
),
因为λ≠0,所以
=-
+
,
又由x2
+x
-
=
,得
=x2
+x
,
根据平面向量基本定理,有
,
消去λ,得x2+x-1=0,从而x=
.
故选D.
| AB |
| BC |
| OB |
| OA |
| OC |
| OB |
因为λ≠0,所以
| OC |
| 1 |
| λ |
| OA |
| 1+λ |
| λ |
| OB |
又由x2
| OA |
| OB |
| OC |
| 0 |
| OC |
| OA |
| OB |
根据平面向量基本定理,有
|
消去λ,得x2+x-1=0,从而x=
-1±
| ||
| 2 |
故选D.
点评:1.本题考查了共线向量定理、平面向量基本定理,关键是利用向量运算法则,对共线向量的充要条件进行灵活变形,将向量关系转化为实数的关系.
2.记住一些常用的结论,可加快解题的速度,如A、B、C三点共线,O为直线ABC外一点,则存在不为零的实数λ1,λ2,λ3,使得λ1
+λ2
+λ3
=
,且λ1+λ2+λ3=0,根据这一规律,本题还可以快速求解:由
=λ
知,A、B、C三点共线,x2+x-1=0,解方程即得解集.
2.记住一些常用的结论,可加快解题的速度,如A、B、C三点共线,O为直线ABC外一点,则存在不为零的实数λ1,λ2,λ3,使得λ1
| OA |
| OB |
| OC |
| 0 |
| AB |
| BC |

练习册系列答案
相关题目
下列命题中真命题是( )
| A、?x0∈R,ex0≤0 | ||
| B、?x∈R,2x>x2 | ||
C、若a<1,则
| ||
| D、a>1,b>1是ab>1的充分条件 |
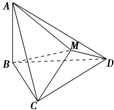 如图,△BCD与△MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2
如图,△BCD与△MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2