题目内容
已知数列{an}是等差数列，a20=a16+8，且a1，a3，a4成等比数列，则a2= ．
考点：等差数列与等比数列的综合
专题：等差数列与等比数列
分析：由已知得
，由此能求出数列的首项和公差，从而能求出a2．
|
解答：
解：∵数列{an}是等差数列，a20=a16+8，且a1，a3，a4成等比数列，
∴
，
解得d=2，a1=-8，
∴a2=-8+2=-6．
故答案为：-6．
∴
|
解得d=2，a1=-8，
∴a2=-8+2=-6．
故答案为：-6．
点评：本题考查数列的第2项的求法，是中档题，解题时要注意等差数列和等比数列的性质的合理运用．
练习册系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
设函数f（x）=logax（a＞0且a≠1），若f（x1•x2•x3…x2015）=50，则f（x12）+f（x22）+f（x32）+…+f（x20152）的值等于（ ）
| A、10 | B、100 |
| C、1000 | D、2015 |
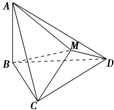如图，△BCD与△MCD都是边长为2的正三角形，平面MCD⊥平面BCD，AB⊥平面BCD，AB=2