题目内容
已知
=(sinx,-cosx),
=(cosx,
cosx),函数f(x)=
•
+
.
(1)求f(x)的最小正周期及单调递减区间;
(2)当0≤x≤
时,求函数f(x)的值域.
| a |
| b |
| 3 |
| a |
| b |
| ||
| 2 |
(1)求f(x)的最小正周期及单调递减区间;
(2)当0≤x≤
| π |
| 2 |
考点:平面向量数量积的运算,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质,平面向量及应用
分析:(1)利用向量的数量积运算法则、倍角公式、两角和差的正弦公式、周期性、正弦函数的单调性即可得出;
(2)当0≤x≤
时,可得-
≤2x-
≤
,利用正弦函数的单调性可得-
≤sin(2x-
)≤1,即可得到函数f(x)的值域.
(2)当0≤x≤
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
| ||
| 2 |
| π |
| 3 |
解答:
解:(1)函数f(x)=
•
+
=sinxcosx-
cos2x+
=
sin2x-
+
=sin(2x-
),
∴T=
=π.
由
+2kπ≤2x-
≤
+2kπ(k∈Z),解得
+kπ≤x≤
+kπ,
∴函数f(x)的单调递减区间为[
+kπ,
+kπ](k∈Z);
(2)当0≤x≤
时,-
≤2x-
≤
,
∴-
≤sin(2x-
)≤1,
∴函数f(x)的值域是[-
,1].
| a |
| b |
| ||
| 2 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
=sin(2x-
| π |
| 3 |
∴T=
| 2π |
| 2 |
由
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
| 5π |
| 12 |
| 11π |
| 12 |
∴函数f(x)的单调递减区间为[
| 5π |
| 12 |
| 11π |
| 12 |
(2)当0≤x≤
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
∴-
| ||
| 2 |
| π |
| 3 |
∴函数f(x)的值域是[-
| ||
| 2 |
点评:本题考查了向量的数量积运算法则、倍角公式、两角和差的正弦公式、周期性、正弦函数的单调性等基础知识与基本技能方法,属于中档题.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
已知箱中共有6个球,其中红球、黄球、蓝球各2个.每次从该箱中取1个球 (有放回,每球取到的机会均等),共取三次.设事件A:“第一次取到的球和第二次取到的球颜色相同”,事件B:“三次取到的球颜色都相同”,则P(B|A)=( )
A、
| ||
B、
| ||
C、
| ||
| D、1 |
下列各式中正确的是( )
(1)(λ•
)•
=λ•(
)=
•(λ
)
(2)|
•
|=|
|•|
|
(3)(
•
)•
=
•(
•
)
(4)(
+
)•
=
•
+
•
.
(1)(λ•
| a |
| b |
| a |
| b |
| a |
| b |
(2)|
| a |
| b |
| a |
| b |
(3)(
| a |
| b |
| c |
| a |
| b |
| c |
(4)(
| a |
| b |
| c |
| a |
| c |
| b |
| c |
| A、(1)(3) |
| B、(2)(4) |
| C、(1)(4) |
| D、以上都不对 |
过点A(-2,0)的直线交圆x2+y2=1交于P、Q两点,则
•
的值为( )
| AP |
| AQ |
| A、3 | B、1 | C、5 | D、4 |
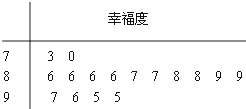 前不久,省社科院发布了2013年度“安徽城市居民幸福排行榜”,芜湖市成为本年度安徽最“幸福城”.随后,师大附中学生会组织部分同学,用“10分制”随机调查“阳光”社区人们的幸福度.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
前不久,省社科院发布了2013年度“安徽城市居民幸福排行榜”,芜湖市成为本年度安徽最“幸福城”.随后,师大附中学生会组织部分同学,用“10分制”随机调查“阳光”社区人们的幸福度.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):