Question

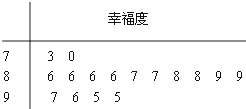前不久，省社科院发布了2013年度“安徽城市居民幸福排行榜”，芜湖市成为本年度安徽最“幸福城”．随后，师大附中学生会组织部分同学，用“10分制”随机调查“阳光”社区人们的幸福度．现从调查人群中随机抽取16名，如图所示的茎叶图记录了他们的幸福度分数（以小数点前的一位数字为茎，小数点后的一位数字为叶）：
（Ⅰ）指出这组数据的众数和中位数；
（Ⅱ）若幸福度不低于9.5分，则称该人的幸福度为“极幸福”．求从这16人中随机选取3人，至多有1人是“极幸福”的概率；
（Ⅲ）以这16人的样本数据来估计整个社区的总体数据，若从该社区（人数很多）任选3人，记ξ表示抽到“极幸福”的人数，求ξ的分布列及数学期望．

Answer 1

考点：离散型随机变量的期望与方差,茎叶图

专题：概率与统计

分析：（1）根据所给的茎叶图看出16个数据，找出众数和中位数，中位数需要按照从小到大的顺序排列得到结论．
（2）由题意知本题是一个古典概型，至多有1人是“极幸福”包括有一个人是极幸福和有零个人是极幸福，根据古典概型公式得到结果．
（3）由于从该社区任选3人，记ξ表示抽到“极幸福”学生的人数，得到变量的可能取值是0、1、2、3，结合变量对应的事件，算出概率，写出分布列和期望．

解答： 解：（Ⅰ）众数：8.6；中位数：8.75；                                      
（Ⅱ）设A_i表示所取3人中有i个人是“极幸福”，至多有1人是“极幸福”记为事件A，则P(A)=P(A0)+P(A1)=

C 3 12

C 3 16

+

C 1 4 C 2 12

C 3 16

=

121

140

；                      
（Ⅲ）ξ的可能取值为0，1，2，3．
P(ξ=0)=(

3

4

)3=

27

64

；P(ξ=1)=

C

1 3

1

4

(

3

4

)2=

27

64

；
P(ξ=2)=

C

2 3

(

1

4

)2

3

4

=

9

64

；P(ξ=3)=(

1

4

)3=

1

64

．
则ξ的分布列为：

ξ	0	1	2	3
P	27 64	27 64	9 64	1 64

所以Eξ=0×

27

64

+1×

27

64

+2×

9

64

+3×

1

64

=0.75．
另解：ξ的可能取值为0，1，2，3．
则ξ～B（3，

1

4

），P(ξ=k)=

C

k 3

(

1

4

)k(

3

4

)3-k．所以Eξ=3×

1

4

=0.75．

点评：本题是一个统计综合题，对于一组数据，通常要求的是这组数据的众数，中位数，平均数，题目分别表示一组数据的特征，这样的问题可以出现在选择题或填空题，考查最基本的知识点．