题目内容
给出下列四个结论,其中正确的是( )
A、若
| ||||||
| B、“a=3”是“直线l1:a2x+3y-1=0与直线l2:x-3y+2=0垂直”的充要条件 | ||||||
| C、对于命题P:?x∈R使得x2+x+1<0,则¬P:?x∈R均有x2+x+1>0 | ||||||
D、在区间[0,1]上随机取一个数x,sin
|
考点:命题的真假判断与应用
专题:阅读型,简易逻辑
分析:可通过举反例判断A;先求出两直线垂直的等价条件,再通过充分必要条件来判断B;由含有一个量词的命题的否定来判断C;根据几何概率的定义,先解0≤sin
≤
,得到0≤x≤
,再由长度之比,即可得到所求概率,从而判断D.
| πx |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
解答:
解:A.若
>
,可举a=1,b=-1,满足条件,但a>b,故A错;
B.由直线l1:a2x+3y-1=0与直线l2:x-3y+2=0垂直得,(-
)•
=-1,解得a=±3,故“a=3”是“直线l1:a2x+3y-1=0与直线l2:x-3y+2=0垂直”的充分不必要条件,即B错;
C.对于命题P:?x∈R使得x2+x+1<0,则¬P:?x∈R均有x2+x+1≥0,故C错;
D.在区间[0,1]上随机取一个数x,sin
x的值介于0到
之间,即0≤sin
≤
,解得0≤x≤
,故所求概率为
.即D正确.
故选D.
| 1 |
| a |
| 1 |
| b |
B.由直线l1:a2x+3y-1=0与直线l2:x-3y+2=0垂直得,(-
| a2 |
| 3 |
| 1 |
| 3 |
C.对于命题P:?x∈R使得x2+x+1<0,则¬P:?x∈R均有x2+x+1≥0,故C错;
D.在区间[0,1]上随机取一个数x,sin
| π |
| 2 |
| 1 |
| 2 |
| πx |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
故选D.
点评:本题主要考查充分必要条件和含一个量词的命题的否定,同时考查不等式的性质和几何概率的求法,属于基础题.

练习册系列答案
相关题目
为了解某班学生喜爱打篮球是否与性别有关,对该班50名学生进行了问卷调查,得到如下的2×2列联表.
则至少有( )的把握认为喜爱打篮球与性别有关.
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
| A、95% | B、99% |
| C、99.5% | D、99.9% |
i是虚数单位,复数
的虚部为( )
| -2i |
| 1+i |
| A、2 | B、-1 | C、1 | D、-2 |
在等差数列{an}中,已知a3+a9=16,则该数列前11项和S11=( )
| A、58 | B、88 |
| C、143 | D、176 |
已知集合U={-1,0,1},A={1},B⊆U,则B∩(∁UA)不可能为( )
| A、∅ | B、{0} |
| C、{-1,0} | D、{-1,0,1} |
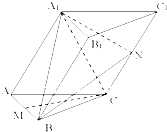 己知斜三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧面A1ACC1为菱形,∠A1AC=60°,平面A1ACC1⊥平面ABC,M、N是AB,CC1的中点.
己知斜三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧面A1ACC1为菱形,∠A1AC=60°,平面A1ACC1⊥平面ABC,M、N是AB,CC1的中点.