题目内容
已知抛物线y2=2px(p>0),过原点分别作斜率是k1,k2的直线,交抛物线于A,B两点,直线AB与x轴的交点为M(x0,0)
(1)若k1•k2=-2,直线AB是否过定点?同时求△AOB面积的最小值;
(2)若∠AOB=
,求x0的最小值.
(1)若k1•k2=-2,直线AB是否过定点?同时求△AOB面积的最小值;
(2)若∠AOB=
| π |
| 3 |
考点:抛物线的简单性质
专题:圆锥曲线中的最值与范围问题
分析:(1)由题意可设直线AB的方程为:my=x-x0.与抛物线方程联立可得根与系数的关系、利用斜率公式即可得出x0,再利用弦长公式、点到直线的距离公式、三角形的面积计算公式即可得出;
(2)利用(1)的结论、斜率计算公式、两角和的正切公式、一元二次方程的解法即可得出.
(2)利用(1)的结论、斜率计算公式、两角和的正切公式、一元二次方程的解法即可得出.
解答:
解:(1)由题意可设直线AB的方程为:my=x-x0.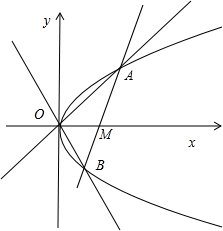
联立
,化为y2-2pmy-2px0=0,
∴y1+y2=2pm,y1y2=-2px0.
∵k1=
,k2=
,k1k2=-2.
∴
=-2.
∴y1y2=-2x1x2,
又x1x2=(my1+x0)(my2+x0)=m2y1y2+mx0(y1+y2)+
=-2pm2x0+2pm2x0+
=
.
∴-2px0=-2
,
∵x0≠0,∴x0=p.
因此直线AB过定点M(p,0).
∵|AB|=
=
,
点O到直线AB的距离d=
.
∴△AOB面积S=
|AB|•d=
×
×
=p2
≥
p2.
因此当m=0时,△AOB的面积取得最小值
p2.
(2)由(1)可得:y1+y2=2pm,y1y2=-2px0.
∵k1=
=tan∠AOM,k2=
=tan[π-(
-∠AOM)]=tan(
+∠AOM)=
=
,
∴k2+
k1k2=-
+k1.
∴
+
=-
+
,
化为y2x1+
y1y2=y1x2-
x1x2
又x1x2=(my1+x0)(my2+x0)=m2y1y2+mx0(y1+y2)+
=-2pm2x0+2pm2x0+
=
.
y2x1=y2(my1+x0)=my1y2+y2x0,y1x2=y1(my2+x0)=my1y2+y1x0.
∴my1y2+x0y2+
y1y2=my1y2+y1x0-
.
∴x0y2-2
px0=y1x0-
,
∵x0≠0,
∴
(x0-2p)=y1-y2.
当y1<y2时,
∴3(x0-2p)2=(y1-y2)2=(y1+y2)2-4y1y2=4p2m2+8px0.
化为3
-20px0+12p2-4p2m2=0,
解得x0=
=
≥
∴x0的最小值为
.

联立
|
∴y1+y2=2pm,y1y2=-2px0.
∵k1=
| y1 |
| x1 |
| y2 |
| x2 |
∴
| y1y2 |
| x1x2 |
∴y1y2=-2x1x2,
又x1x2=(my1+x0)(my2+x0)=m2y1y2+mx0(y1+y2)+
| x | 2 0 |
| x | 2 0 |
| x | 2 0 |
∴-2px0=-2
| x | 2 0 |
∵x0≠0,∴x0=p.
因此直线AB过定点M(p,0).
∵|AB|=
| (1+m2)[(y1+y2)2-4y1y2] |
| (1+m2)[4p2m2+8p2] |
点O到直线AB的距离d=
| p | ||
|
∴△AOB面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| (1+m2)(4p2m2+8p2) |
| p | ||
|
| m2+2 |
| 2 |
因此当m=0时,△AOB的面积取得最小值
| 2 |
(2)由(1)可得:y1+y2=2pm,y1y2=-2px0.
∵k1=
| y1 |
| x1 |
| y2 |
| x2 |
| π |
| 3 |
| 2π |
| 3 |
-
| ||
1+
|
-
| ||
1+
|
∴k2+
| 3 |
| 3 |
∴
| y2 |
| x2 |
| ||
| x1x2 |
| 3 |
| y1 |
| x1 |
化为y2x1+
| 3 |
| 3 |
又x1x2=(my1+x0)(my2+x0)=m2y1y2+mx0(y1+y2)+
| x | 2 0 |
| x | 2 0 |
| x | 2 0 |
y2x1=y2(my1+x0)=my1y2+y2x0,y1x2=y1(my2+x0)=my1y2+y1x0.
∴my1y2+x0y2+
| 3 |
| 3 |
| x | 2 0 |
∴x0y2-2
| 3 |
| 3 |
| x | 2 0 |
∵x0≠0,
∴
| 3 |
当y1<y2时,
∴3(x0-2p)2=(y1-y2)2=(y1+y2)2-4y1y2=4p2m2+8px0.
化为3
| x | 2 0 |
解得x0=
20p±4p
| ||
| 6 |
10p±2p
| ||
| 3 |
| 2p |
| 3 |
∴x0的最小值为
| 2p |
| 3 |
点评:本题综合考查了直线与抛物线相交问题转化为方程联立可得根与系数的关系、斜率公式、弦长公式、点到直线的距离公式、三角形的面积计算公式、两角和的正切公式、一元二次方程的解法等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
给出下列四个结论,其中正确的是( )
A、若
| ||||||
| B、“a=3”是“直线l1:a2x+3y-1=0与直线l2:x-3y+2=0垂直”的充要条件 | ||||||
| C、对于命题P:?x∈R使得x2+x+1<0,则¬P:?x∈R均有x2+x+1>0 | ||||||
D、在区间[0,1]上随机取一个数x,sin
|
已知实数x、y满足不等式组
,则z=x-y的最小值为( )
|
| A、-1 | ||
B、-
| ||
| C、-3 | ||
| D、3 |

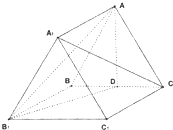 在正三棱柱ABC-A1B1C1中,点D是BC的中点,BC=BB1.
在正三棱柱ABC-A1B1C1中,点D是BC的中点,BC=BB1.