题目内容
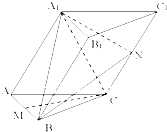 己知斜三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧面A1ACC1为菱形,∠A1AC=60°,平面A1ACC1⊥平面ABC,M、N是AB,CC1的中点.
己知斜三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧面A1ACC1为菱形,∠A1AC=60°,平面A1ACC1⊥平面ABC,M、N是AB,CC1的中点.(I)求证:CM∥平面A1BN.
(Ⅱ)求证:A1C⊥BN.
考点:直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)取A1B的中点P,连接PM,PN.根据M,P分别是AB,A1B的中点,推断u PM∥AA1,PM=
AA1,根据 AA1∥CC1,推断出 PM∥CN且PM=CN可知四边形PMCN为平行四边形,推断出PN∥CM.最后利用线面平行的判定定理推断出CM∥平面A1BN.
(Ⅱ)取AC的中点O,连结BO,ON.根据已知BO⊥AC,进而根据平面A1ACC1⊥平面ABC,推断出BO⊥平面A1ACC1.由于 A1C?平面A1ACC1利用线面垂直性质知BO⊥A1C,利用四边形A1ACC1为菱形,推断 A1C⊥AC1,又因为 ON∥AC1,推断出A1C⊥ON进而推断出A1C⊥平面BON,又BN?平面BON,最后根据线面垂直的判定定理推断出A1C⊥BN.
| 1 |
| 2 |
(Ⅱ)取AC的中点O,连结BO,ON.根据已知BO⊥AC,进而根据平面A1ACC1⊥平面ABC,推断出BO⊥平面A1ACC1.由于 A1C?平面A1ACC1利用线面垂直性质知BO⊥A1C,利用四边形A1ACC1为菱形,推断 A1C⊥AC1,又因为 ON∥AC1,推断出A1C⊥ON进而推断出A1C⊥平面BON,又BN?平面BON,最后根据线面垂直的判定定理推断出A1C⊥BN.
解答:
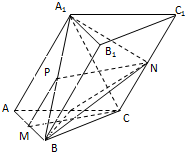
证明:(Ⅰ)取A1B的中点P,连接PM,PN.因为 M,P分别是AB,A1B的中点,
∴PM∥AA1,PM=
AA1,
又∵AA1∥CC1,
∴PM∥CN且PM=CN
∴四边形PMCN为平行四边形,
∴PN∥CM.
又∵CM?平面A1BN,PN?平面A1BN,
∴CM∥平面A1BN.
(Ⅱ)取AC的中点O,连结BO,ON.
由题意知 BO⊥AC,
又∵平面A1ACC1⊥平面ABC,
∴BO⊥平面A1ACC1.
∵A1C?平面A1ACC1
∴所以BO⊥A1C
∴四边形A1ACC1为菱形,
∴A1C⊥AC1
又∵ON∥AC1,所以 A1C⊥ON
∴A1C⊥平面BON,又 BN?平面BON
∴A1C⊥BN.
∴PM∥AA1,PM=
| 1 |
| 2 |

又∵AA1∥CC1,
∴PM∥CN且PM=CN
∴四边形PMCN为平行四边形,
∴PN∥CM.
又∵CM?平面A1BN,PN?平面A1BN,
∴CM∥平面A1BN.
(Ⅱ)取AC的中点O,连结BO,ON.
由题意知 BO⊥AC,
又∵平面A1ACC1⊥平面ABC,
∴BO⊥平面A1ACC1.
∵A1C?平面A1ACC1
∴所以BO⊥A1C
∴四边形A1ACC1为菱形,
∴A1C⊥AC1
又∵ON∥AC1,所以 A1C⊥ON
∴A1C⊥平面BON,又 BN?平面BON
∴A1C⊥BN.
点评:本题主要考查了线面平行的判定定理,线面垂直的性质及判定.要求学生对基础定理和性质熟练掌握.

练习册系列答案
相关题目
给出下列四个结论,其中正确的是( )
A、若
| ||||||
| B、“a=3”是“直线l1:a2x+3y-1=0与直线l2:x-3y+2=0垂直”的充要条件 | ||||||
| C、对于命题P:?x∈R使得x2+x+1<0,则¬P:?x∈R均有x2+x+1>0 | ||||||
D、在区间[0,1]上随机取一个数x,sin
|