题目内容
在等差数列{an}中，已知a3+a9=16，则该数列前11项和S11=（ ）
| A、58 | B、88 |
| C、143 | D、176 |
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：根据等差数列的性质可知a1+a11=a3+a9，然后根据等差数列的求和公式解之即可求出所求．
解答：
解：∵等差数列{an}，
∴a1+a11=a3+a9=16，
则S11=
×11=8×11=88．
故选：B．
∴a1+a11=a3+a9=16，
则S11=
| a1+a11 |
| 2 |
故选：B．
点评：本题主要考查了等差数列的性质，以及等差数列的求和公式，熟练掌握性质及公式是解本题的关键，属于基础题．
练习册系列答案
相关题目
设集合M={0，1，2}，N={x|x2-3x+2≤0}，则M∩N=（ ）
| A、{1} | B、{2} |
| C、{0，1} | D、{1，2} |
给出下列四个结论，其中正确的是（ ）
A、若
| ||||||
| B、“a=3”是“直线l1：a2x+3y-1=0与直线l2：x-3y+2=0垂直”的充要条件 | ||||||
| C、对于命题P：?x∈R使得x2+x+1＜0，则￢P：?x∈R均有x2+x+1＞0 | ||||||
D、在区间[0，1]上随机取一个数x，sin
|
若复数z1=1+i，z2=2i，则
=（ ）
| z2 |
| z1 |
| A、-1+i | B、1+i |
| C、-2+2i | D、2+2i |
已知i为虚数单位，则复数z=
在复平面内表示的点位于（ ）
| -5i |
| 2+3i |
| A、第四象限 | B、第三象限 |
| C、第二象限 | D、第一象限 |
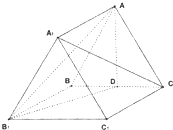在正三棱柱ABC-A1B1C1中，点D是BC的中点，BC=BB1．