题目内容
等比数列{an}的前n项和为Sn，已知S1，2S2，3S3成等差数列，则
= ．
| S3 |
| a2 |
考点：等差数列与等比数列的综合
专题：计算题,等差数列与等比数列
分析：根据已知先求出q的值，从而即可求出
的值．
| S3 |
| a2 |
解答：
解：设首项为a1，公比为q
S1=a1
S2=a1+qa1
S3=a1+qa1+q2a1
因为，S1，2S2，3S3成等差
则：4S2=S1+3S3
⇒4a1+4qa1=a1+3a1+3qa1+3q2 a1
⇒3q2 a1-qa1=0
⇒q（3q-1）=0
因为，q不等于0
所以，q=
，从而有
=
=
=
．
故答案为：
．
S1=a1
S2=a1+qa1
S3=a1+qa1+q2a1
因为，S1，2S2，3S3成等差
则：4S2=S1+3S3
⇒4a1+4qa1=a1+3a1+3qa1+3q2 a1
⇒3q2 a1-qa1=0
⇒q（3q-1）=0
因为，q不等于0
所以，q=
| 1 |
| 3 |
| S3 |
| a2 |
| a1+qa1+q2a1 |
| qa1 |
1+
| ||||
|
| 13 |
| 3 |
故答案为：
| 13 |
| 3 |
点评：本题主要考察了等差数列与等比数列的综合应用，考察了计算能力，属于中档题．
练习册系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
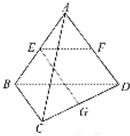如图所示，已知空间四边形ABCD的每条边和对角线长都等于1，点E、F、G分别是AB、AD、CD的中点，计算：（1）
| EF |
| BA |
（2）
| EF |
| DC |
（3）EG的长；
（4）异面直线AG与CE所成角的余弦值．
函数f（x）=（4-x）ex的单调递减区间是（ ）
| A、（-∞，4） |
| B、（-∞，3） |
| C、（4，+∞） |
| D、（3，+∞） |