题目内容
已知t为自变量,求下列函数的二阶导数.
(1)u=A•e-
;
(2)u=
;
(3)u=
.
(1)u=A•e-
| B |
| t |
(2)u=
| A+B |
| lg(1+t) |
(3)u=
| t |
| A+Bt |
考点:导数的运算
专题:导数的概念及应用
分析:根据求导法则和复合函数的求导法则,求导即可,
解答:
解:(1)∵u′=(A•e-
)′=e-
•
,
∴u″=e-
•
•
+e-
•(-
)=e-
•
•(
-2t),
(2)∵u′=
,
∴u″=(A+B)(-
)=-(A+B)•
(3)∵u′=
=
=A•(A+Bt)-2,
u″=A•(-2)•(A+Bt)-3•B=-
| B |
| t |
| B |
| t |
| B |
| t2 |
∴u″=e-
| B |
| t |
| B |
| t2 |
| B |
| t2 |
| B |
| t |
| 2tB |
| t2 |
| B |
| t |
| B |
| t2 |
| B |
| t2 |
(2)∵u′=
(A+B)•
| ||
| lg2(1+t) |
∴u″=(A+B)(-
| lg2(1+t)+2lg(1+t) |
| lg4(1+t)(1+t)2 |
| lg(1+t)+2 |
| (1+t)2lg2(1+t) |
(3)∵u′=
| (A+Bt)-Bt |
| (A+Bt)2 |
| A |
| (A+Bt)2 |
u″=A•(-2)•(A+Bt)-3•B=-
| 2AB |
| (A+Bt)3 |
点评:本题主要考查求函数的导数的方法,属于基础题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
已知双曲线
-y2=1(a>0)的实轴长2,则该双曲线的离心率为( )
| x2 |
| a |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
以下说法正确的是( )
| A、若直线a不平行于平面α,则直线a与平面α相交 |
| B、直线a和b是异面直线,若直线c∥a,则c与b一定相交 |
| C、若直线a和b都和平面α平行,则a和b也平行 |
| D、若直线c平行直线a,直线b⊥a,则b⊥c |
 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,E、F分别是PB、CD的中点,且PB=PC=PD=4.
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,E、F分别是PB、CD的中点,且PB=PC=PD=4.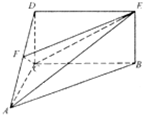 如图,四边形BCDE为矩形,平面ABC⊥平面BCDE,AC⊥BC,AC=CD=
如图,四边形BCDE为矩形,平面ABC⊥平面BCDE,AC⊥BC,AC=CD=