题目内容
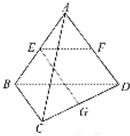如图所示，已知空间四边形ABCD的每条边和对角线长都等于1，点E、F、G分别是AB、AD、CD的中点，计算：（1）
| EF |
| BA |
（2）
| EF |
| DC |
（3）EG的长；
（4）异面直线AG与CE所成角的余弦值．
考点：平面向量数量积的运算,异面直线及其所成的角
专题：平面向量及应用,空间角
分析：（1）由数量积的定义得到
•
=EF×AB×cos60°，计算即可
（2）由题意作图，可得
•
数量积为
•
，由已知易得其模长和夹角，由数量积的定义可得．
（3）由题意，得到△EFG是等腰直角三角形，即可求EG的长度；
（4）利用向量的数量积公式，求出向量
与
的夹角的余弦值，即可求异面直线AG与CE所成角的余弦值．
| EF |
| BA |
（2）由题意作图，可得
| EF |
| DC |
| 1 |
| 2 |
| BD |
| CD |
（3）由题意，得到△EFG是等腰直角三角形，即可求EG的长度；
（4）利用向量的数量积公式，求出向量
| AG |
| CE |
解答：
解：（1）因为空间四边形ABCD的每条边和对角线长都等于1，点E、F、G分别是AB、AD、CD的中点，
所以
•
=EF×AB×cos60°=
BD×AB×cos60°=
；
（2）
•
=-
•
=-
BD×CD×cos60°=-
；
（3）因为空间四边形ABCD的每条边和对角线长都等于1，点E、F、G分别是AB、AD、CD的中点，
所以EF=FG=
，
作AH⊥BD，则H 为BD的中点，所以CH⊥BD，所以BD⊥平面ACH，所以AC⊥BD，
所以EF⊥FG，
所以EG=
EF=
；
（4）设向量
=
（
+
），
=
（
+
），
因为AC=1，＜
，
＞=120°，＜
，
＞=120°，＜
，
＞=90°，
所以cos＜
，
＞=
=
=
=-
，
所以异面直线AG与CE所成角的余弦值
．
所以
| EF |
| BA |
| 1 |
| 2 |
| 1 |
| 4 |
（2）
| EF |
| DC |
| 1 |
| 2 |
| BD |
| CD |
| 1 |
| 2 |
| 1 |
| 4 |
（3）因为空间四边形ABCD的每条边和对角线长都等于1，点E、F、G分别是AB、AD、CD的中点，
所以EF=FG=
| 1 |
| 2 |
作AH⊥BD，则H 为BD的中点，所以CH⊥BD，所以BD⊥平面ACH，所以AC⊥BD，
所以EF⊥FG，
所以EG=
| 2 |
| ||
| 2 |
（4）设向量
| AG |
| 1 |
| 2 |
| AC |
| AD |
| CE |
| 1 |
| 2 |
| CA |
| CB |
因为AC=1，＜
| AC |
| CB |
| AD |
| CA |
| AD |
| CB |
所以cos＜
| AG |
| CE |
| ||||||||||
|
|
| ||||||||||||||||
|
|
| ||||||||
|
| 2 |
| 3 |
所以异面直线AG与CE所成角的余弦值
| 2 |
| 3 |
点评：本题考查了正四面体中的线线关系以及空间距离和空间角的求法，借助于向量解决空间距离或者空间角是常用方法，题目典型，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
在长方形ABCD中，AB=3，BC=1，E为DC的三等分点（靠近C处），F为线段EC上一动点（包括端点），现将△AFD沿AF折起，使D点在平面内的摄影恰好落在边AB上，则当F运动时，二面角D-AF-B平面角余弦值的变化范围是