题目内容
设函数f（x）=x3+sinx，若0≤θ≤
时，f（mcosθ）+f（1-m）＞0恒成立，则实数m的取值范围是 ．
| π |
| 2 |
考点：函数单调性的性质
专题：函数的性质及应用
分析：利用函数f（x）=x3+sinx是奇函数又是[0，
]上的增函数，把不等式转化求解．
| π |
| 2 |
解答：
解：∵函数f（x）=x3+sinx是奇函数又是[0，
]上的增函数，
∴f（mcosθ）+f（1-m）＞0恒成立，等价于f（mcosθ）＞-f（1-m）
即f（mcosθ）＞f（m-1）即mcosθ＞m-1⇒m＜
又0≤θ≤
时，0≤cosθ≤1，∴m＜1．
故答案为（-∞，1）．
| π |
| 2 |
∴f（mcosθ）+f（1-m）＞0恒成立，等价于f（mcosθ）＞-f（1-m）
即f（mcosθ）＞f（m-1）即mcosθ＞m-1⇒m＜
| 1 |
| 1-cosθ |
又0≤θ≤
| π |
| 2 |
故答案为（-∞，1）．
点评：考查学生对函数的奇偶性单调性的综合运用以及三角函数的单调性的运用能力，属中档题．
练习册系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目
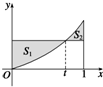在区间[0，1]上给定曲线y=x2，试在此区间内确定点t的值，使图中阴影部分的面积：