题目内容
若不等式x2+2x+2>|a-2|对于一切实数x均成立,则实数a的取值范围是 .
考点:函数恒成立问题
专题:计算题,不等式的解法及应用
分析:构造函数y=x2+2x+2,由二次函数的性质,可以求出函数的最小值,根据不等式x2+2x+2>|a-2|对于一切实数x均成立,可得|a-2|<1,即可得到a的取值范围,进而得到答案.
解答:
解:∵函数y=x2+2x+2的最小值为1,
∴不等式x2+2x+2>|a-2|对于一切实数x均成立,
则|a-2|<1,
∴1<a<3,
∴实数a的取值范围是(1,3).
故答案为:(1,3).
∴不等式x2+2x+2>|a-2|对于一切实数x均成立,
则|a-2|<1,
∴1<a<3,
∴实数a的取值范围是(1,3).
故答案为:(1,3).
点评:本题考查的知识点函数恒成立问题,其中根据二次函数的性质得到函数y=x2+2x+2的最小值是解答本题的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
设f(x)=ax2+(b-8)x-a-ab,若不等式f(x)<0的解集是(-∞,-3)∪(2,+∞),则a+b=( )
| A、-8 | B、-2 | C、8 | D、2 |
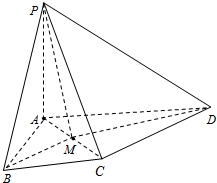 如图所示,PA⊥平面ABCD,△ABC为等边三角形,AP=AB,AC⊥CD,M为AC的中点.
如图所示,PA⊥平面ABCD,△ABC为等边三角形,AP=AB,AC⊥CD,M为AC的中点. 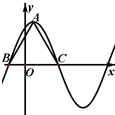 函数f(x)=2
函数f(x)=2