题目内容
已知函数f(x)=
x3-2x2+ax+b的图象在点P(3,f(3)),处的切线方程为y=3x-5.
(Ⅰ)求实数a,b的值;
(Ⅱ)设g(x)=f(x)+
.
①若g(x)是[3,+∞)上的增函数,求实数m的最大值;
②是否存在点Q,使得过点Q的直线若能与曲线y=g(x)围成两个封闭图形,则这两个封闭图形的面积总相等.若存在,求出点Q坐标;若不存在,说明理由.
| 1 |
| 3 |
(Ⅰ)求实数a,b的值;
(Ⅱ)设g(x)=f(x)+
| m |
| x-2 |
①若g(x)是[3,+∞)上的增函数,求实数m的最大值;
②是否存在点Q,使得过点Q的直线若能与曲线y=g(x)围成两个封闭图形,则这两个封闭图形的面积总相等.若存在,求出点Q坐标;若不存在,说明理由.
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(Ⅰ)利用曲线上的点的切线方程与改点的导数的关系问题即可求得;
(Ⅱ)利用函数的单调性转化为恒成立问题,解含m的不等式求m的最值;求得函数图象的对称中心,利用对称性说明.
(Ⅱ)利用函数的单调性转化为恒成立问题,解含m的不等式求m的最值;求得函数图象的对称中心,利用对称性说明.
解答:
解:(Ⅰ)x=3时,f(3)=3a+b-9
∵f′(x)=x2-4x+a,
∴f′(3)=9-12+a,
∴a=6
又∵点P(3,f(3))在直线y=3x-5上,
∴f(3)=4,即3a+b-9=4,
∴b=-5
∴a=6,b=-5,
∴f(x)=
x3-2x2+6x-5.
(Ⅱ)①g(x)=
x3-2x2+6x-5+
.
又g(x)是[3,+∞)上的增函数,
∴g′(x)=x2-4x+6-
=(x-2)2-
+2≥0,在[3,+∞)上恒成立,
令(x-2)2=t,则t≥1,
设y=t-
+2,
∴t-
+2≥0在[1,+∞)上恒成立,
即m≤t2+2t=(t+1)2-1恒成立,
∴m≤3,
故实数m的最大值是3.
②∵g(x)=
x3-2x2+6x-5+
,
∴g(4-x)=
(4-x)3-2(4-x)2+6(4-x)-5+
=-
x3+2x2-6x-
-
,
∴g(x)+g(4-x)=
,
∴Q(2,
)
表明:若点A(x,y)为g(x)图象上任意一点,则点(4-x,
-y)也在图象上,
而线段AB的中点恒为Q(2,
);
由此可知g(x)图象关于点Q(2,
)对称.
这也表明存在点Q(2,
),使得过Q的直线若能与g(x)图象相交围成封闭图形,
则这两个封闭图形面积相等.
∵f′(x)=x2-4x+a,
∴f′(3)=9-12+a,
∴a=6
又∵点P(3,f(3))在直线y=3x-5上,
∴f(3)=4,即3a+b-9=4,
∴b=-5
∴a=6,b=-5,
∴f(x)=
| 1 |
| 3 |
(Ⅱ)①g(x)=
| 1 |
| 3 |
| m |
| x-2 |
又g(x)是[3,+∞)上的增函数,
∴g′(x)=x2-4x+6-
| m |
| (x-2)2 |
| m |
| (x-2)2 |
令(x-2)2=t,则t≥1,
设y=t-
| m |
| t |
∴t-
| m |
| t |
即m≤t2+2t=(t+1)2-1恒成立,
∴m≤3,
故实数m的最大值是3.
②∵g(x)=
| 1 |
| 3 |
| m |
| x-2 |
∴g(4-x)=
| 1 |
| 3 |
| m |
| 4-x-2 |
| 1 |
| 3 |
| 25 |
| 3 |
| m |
| x-2 |
∴g(x)+g(4-x)=
| 10 |
| 3 |
∴Q(2,
| 5 |
| 3 |
表明:若点A(x,y)为g(x)图象上任意一点,则点(4-x,
| 10 |
| 3 |
而线段AB的中点恒为Q(2,
| 5 |
| 3 |
由此可知g(x)图象关于点Q(2,
| 5 |
| 3 |
这也表明存在点Q(2,
| 5 |
| 3 |
则这两个封闭图形面积相等.
点评:考查利用导数求过曲线上点的切线方程的方法,以及利用函数的单调性求字母的最值问题和图象的对称问题,属综合性很强的题目,属难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知角α的终边与单位圆交于点P(m,n),且n=2m(m≠0)那么sin2α的值是( )
A、-
| ||
B、
| ||
C、-
| ||
D、
|
 如图,在三棱锥A-BCD中,BA=BD,AD⊥CD,E、F分别为AC、AD的中点.
如图,在三棱锥A-BCD中,BA=BD,AD⊥CD,E、F分别为AC、AD的中点.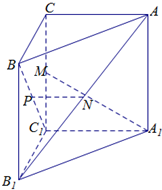 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,且∠ACB=90°,∠BAC=30°,BC=1,AA1=
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,且∠ACB=90°,∠BAC=30°,BC=1,AA1=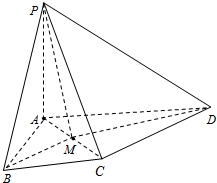 如图所示,PA⊥平面ABCD,△ABC为等边三角形,AP=AB,AC⊥CD,M为AC的中点.
如图所示,PA⊥平面ABCD,△ABC为等边三角形,AP=AB,AC⊥CD,M为AC的中点.