题目内容
某渔轮在航行中不幸遇险,发出呼救信号,我海军舰艇在A处获悉后,测得该渔轮在北偏东45°、距离为10海里的C处,并测得渔轮正沿南偏东75°的方向、以每小时9海里的速度向附近的小岛靠拢.我海军舰艇立即以每小时21海里的速度沿直线方向前去营救;则舰艇靠近渔轮所需的时间是多少小时?
考点:余弦定理的应用
专题:应用题,解三角形
分析:可先根据题意,画出图形,不难得出∠ACB=120°,已知了军舰和渔船的速度,那么可设时间,并用时间表示出AB,BC的长,已知了AC的长为10,可根据余弦定理来求出时间的值.
解答:
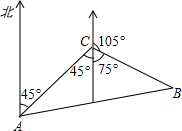 解:设舰艇收到信号后xh在B处靠拢渔轮,
解:设舰艇收到信号后xh在B处靠拢渔轮,
则AB=21x,BC=9x,
又AC=10,∠ACB=45°+75°=120°.
由余弦定理,得AB2=AC2+BC2-2AC•BCcos∠ACB,
即 (21x)2=102+(9x)2-2×10×9xcos∠120°
化简得36x2-9x-10=0,
解得x=
(负值舍去).
答:舰艇经过
小时就可靠近渔轮.
 解:设舰艇收到信号后xh在B处靠拢渔轮,
解:设舰艇收到信号后xh在B处靠拢渔轮,则AB=21x,BC=9x,
又AC=10,∠ACB=45°+75°=120°.
由余弦定理,得AB2=AC2+BC2-2AC•BCcos∠ACB,
即 (21x)2=102+(9x)2-2×10×9xcos∠120°
化简得36x2-9x-10=0,
解得x=
| 2 |
| 3 |
答:舰艇经过
| 2 |
| 3 |
点评:本题主要考查了解三角形的实际应用.解题的关键是利用了余弦定理,利用已知的边和角建立方程求得时间.

练习册系列答案
相关题目
 一个几何体的三视图如图所示,求:
一个几何体的三视图如图所示,求: