题目内容
在△ABC中,A,B,C所对的边分别为a,b,c,且a=3,b=2
,B=2A.
(1)求cosA的值;
(2)求c的值.
| 6 |
(1)求cosA的值;
(2)求c的值.
考点:余弦定理
专题:计算题,解三角形
分析:(1)依题意,利用正弦定理
=
及二倍角的正弦即可求得cosA的值;
(2)易求sinA=
,sinB=
,从而利用两角和的正弦可求得sin(A+B)=
,在△ABC中,此即sinC的值,利用正弦定理可求得c的值.
| 3 |
| sinA |
2
| ||
| sin2A |
(2)易求sinA=
| ||
| 3 |
2
| ||
| 3 |
5
| ||
| 9 |
解答:
解:(1)∵△ABC中,a=3,b=2
,B=2A,
∴由正弦定理得:
=
,即
=
,
∴cosA=
;
(2)由(1)知cosA=
,A∈(0,π),
∴sinA=
,又B=2A,
∴cosB=cos2A=2cos2A-1=
,B∈(0,π),
∴sinB=
,
在△ABC中,sinC=sin(A+B)=sinAcosB+cosAsinB=
×
+
×
=
,
∴c=
=
=5.
| 6 |
∴由正弦定理得:
| 3 |
| sinA |
2
| ||
| sin2A |
| 2sinAcosA |
| sinA |
2
| ||
| 3 |
∴cosA=
| ||
| 3 |
(2)由(1)知cosA=
| ||
| 3 |
∴sinA=
| ||
| 3 |
∴cosB=cos2A=2cos2A-1=
| 1 |
| 3 |
∴sinB=
2
| ||
| 3 |
在△ABC中,sinC=sin(A+B)=sinAcosB+cosAsinB=
| ||
| 3 |
| 1 |
| 3 |
| ||
| 3 |
2
| ||
| 3 |
5
| ||
| 9 |
∴c=
| asinC |
| sinA |
3×
| ||||
|
点评:本题考查正弦定理,考查两角和的正弦与诱导公式的应用,考查运算求解能力,属于中档题.

练习册系列答案
相关题目
一个几何体的三视图如图所示,则该几何体的体积为( )


A、
| ||
B、
| ||
| C、3 | ||
| D、4 |
二进制数111111(2)化成十进制数的值是( )
| A、63 | B、62 | C、64 | D、61 |
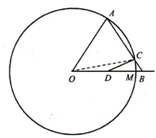 如图,半径为1的圆O上有一定点M,A为圆O上的动点.在射线OM上有一动点B,AB=1,0B>1.线段AB交圆O于另一点C,D为线段的OB中点.求线段CD长的取值范围.
如图,半径为1的圆O上有一定点M,A为圆O上的动点.在射线OM上有一动点B,AB=1,0B>1.线段AB交圆O于另一点C,D为线段的OB中点.求线段CD长的取值范围.