题目内容
已知动点P在椭圆
+
=1上，若A点坐标为（3，0），且|
|=1，且
•
=0，则|
|的最小值是（ ）
| x2 |
| 25 |
| y2 |
| 16 |
| AM |
| PM |
| AM |
| PM |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：由题设条件，结合向量的性质，推导出|
|2=|
|2-|
|2，再由|
|越小，|
|越小，能求出|
|最小值．
| PM |
| AP |
| AM |
| AP |
| PM |
| PM |
解答：
解：∵
•
=0，∴
⊥
=0，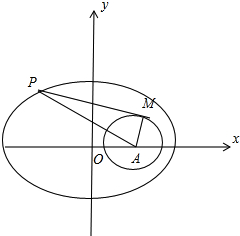
∴|
|2=|
|2-|
|2
∵|
|=1，∴|
|2=1，
∴|
|2=|
|2-|
|2=|
|2-1，
∵|
|=1，
∴点M的轨迹为以为以点A为圆心，1为半径的圆，
∵|
|2=|
|2-1，|
|越小，|
|越小，
结合图形知，当P点为椭圆的右顶点时，
|
|取最小值a-c=5-3=2，
∴|
|最小值是
=
．
故选：B．
| PM |
| AM |
| PM |
| AM |
∴|
| PM |
| AP |
| AM |
∵|
| AM |
| AM |
∴|
| PM |
| AP |
| AM |
| AP |
∵|
| AM |
∴点M的轨迹为以为以点A为圆心，1为半径的圆，
∵|
| PM |
| AP |
| AP |
| PM |
结合图形知，当P点为椭圆的右顶点时，
|
| AP |
∴|
| PM |
| 4-1 |
| 3 |
故选：B．
点评：本题考查椭圆上的线段长的最小值的求法，解题时要认真审题，要熟练掌握椭圆的性质，是中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
函数y=
-sin2x-3cosx的最小值是（ ）
| 5 |
| 4 |
A、-
| ||
| B、-2 | ||
C、
| ||
D、-
|
一个几何体的三视图如图所示，则该几何体的体积为（ ）
A、
| ||
B、
| ||
| C、3 | ||
| D、4 |
设y=x2•ex，则y′等于（ ）
| A、x2ex+2x |
| B、2xex |
| C、（2x+x2）ex |
| D、（x+x2）•ex |
执行如图所示的程序框图，输出的S值为64则“ ”处应填（ ）| A、2 | B、3 | C、4 | D、5 |
已知A（0，-1），B（2，2），C（4，-6），则
在
方向上的投影为（ ）
| AB |
| AC |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
二进制数111111（2）化成十进制数的值是（ ）
| A、63 | B、62 | C、64 | D、61 |