题目内容
20．已知复数z满足$\frac{z}{1+i}=|{2-i}|$，则z的共轭复数对应的点位于复平面内的（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
分析 利用复数的运算法则、几何意义、模的计算公式即可得出．
解答 解：$\frac{z}{1+i}=|{2-i}|$=$\sqrt{5}$，∴z=$\sqrt{5}$+$\sqrt{5}$i．
则z的共轭复数$\sqrt{5}$-$\sqrt{5}$对应的点（$\sqrt{5}$，-$\sqrt{5}$）位于复平面内的第四象限．
故选：D．
点评 本题考查了复数的运算法则、几何意义、模的计算公式，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
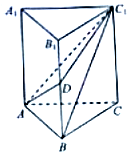如图，在直三棱柱ABC-A1B1C1中，AB=1，BC=2，BB1=3，∠ABC=90°，点D为侧棱BB1上的动点，当AD+DC1最小时，三棱锥D-ABC1的体积为$\frac{1}{3}$．
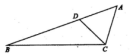如图，在△ABC中，D为线段AB上的点，且AB=3AD，AC=AD，CB=3CD，则$\frac{sin2B}{sinA}$=$\frac{7}{9}$．
5．表是一个容量为10的样本数据分组后的频率分布，若利用组中中近似计算本组数据的平均数$\overline x$，则$\overline x$的值为19.7
| 数据 | [12，5，15.5） | [15.5，18.5） | [18.5，21.5） | [21，5，24.5） |
| 频数 | 2 | 1 | 3 | 4 |