题目内容
已知集合M={x|
≥0}，则∁RM=（ ）
| 1+x |
| 1-x |
| A、{x|-1＜x＜1} |
| B、{x|-1＜x≤1} |
| C、{x|x＜-1或x≥1} |
| D、{x|x≤-1或x≥1} |
考点：补集及其运算
专题：集合
分析：先由不等式性质求出集合M={x|
≥0}={x|-1≤x＜1}，由此能求出∁RM．
| 1+x |
| 1-x |
解答：
解：∵集合M={x|
≥0}={x|-1≤x＜1}，
∴∁RM={x|x＜-1或x≥1}．
故选：C．
| 1+x |
| 1-x |
∴∁RM={x|x＜-1或x≥1}．
故选：C．
点评：本题考查集合的补集的求法，是基础题，解题时要认真审题，注意不等式性质的合理运用．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
若复数z满足iz=2+4i，i为虚数单位，则在复平面内z对应的点的坐标是（ ）
| A、（4，2） |
| B、（4，-2） |
| C、（2，4） |
| D、（2，-4） |
如图，在△ABC中，∠ABC=90°，以AB为直径的圆O交AC于点E，点D是BC边上的中点，连接OD交圆O与点M．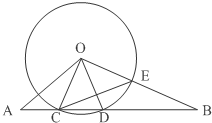
如图，⊙O的半径为6，线段AB与⊙相交于点C、D，AC=4，∠BOD=∠A，OB与⊙O相交于点．