题目内容
已知函数f(x)=
x2+kx+1,g(x)=(x+1)ln(x+1),h(x)=f(x)+g′(x).
(Ⅰ)若函数g(x)的图象在原点处的切线l与函数f(x)的图象相切,求实数k的值;
(Ⅱ)若h(x)在[0,2]上单调递减,求实数k的取值范围;
(Ⅲ)若对于?t∈[0,
-1],总存在x1,x2∈(-1,4),且x1≠x2满f(xi)=g(t)(i=1,2),其中e为自然对数的底数,求实数k的取值范围.
| 1 |
| 2 |
(Ⅰ)若函数g(x)的图象在原点处的切线l与函数f(x)的图象相切,求实数k的值;
(Ⅱ)若h(x)在[0,2]上单调递减,求实数k的取值范围;
(Ⅲ)若对于?t∈[0,
| e |
考点:利用导数研究曲线上某点切线方程,利用导数求闭区间上函数的最值
专题:函数的性质及应用,导数的概念及应用,导数的综合应用,不等式的解法及应用
分析:(Ⅰ)求出g(x)的定义域和导数,求得切线的斜率和切点,写出切线方程,联立f(x),消去y,运用判别式为0,即可得到k;
(Ⅱ)求出h(x)的导数,h(x)在[0,2]上单调递减,则h′(x)≤0对x∈[0,2]恒成立,运用导数求出h′(x)在[0,2]的最大值,解不等式即可得到k的范围;
(Ⅲ)分别求出g(t)在t∈[0,
-1]的值域A和f(x)在x∈(-1,4)的值域B,由题意可得A包含于B,得到不等式组,解出即可得到k的范围.
(Ⅱ)求出h(x)的导数,h(x)在[0,2]上单调递减,则h′(x)≤0对x∈[0,2]恒成立,运用导数求出h′(x)在[0,2]的最大值,解不等式即可得到k的范围;
(Ⅲ)分别求出g(t)在t∈[0,
| e |
解答:
解:(Ⅰ)函数g(x)的定义域为(-1,+∞),
g′(x)=ln(x+1)+1,
则g(0)=0,g′(0)=1,
∴切线l:y=x,
由
⇒x2+2(k-1)x+2=0,
∵l与函数f(x)的图象相切,
∴△=4(k-1)2-8=0⇒k=1±
;
(Ⅱ)h(x)=
x2+kx+1+ln(x+1)+1,导数h′(x)=x+k+
,
令φ(x)=x+k+
,
φ′(x)=1-
=
>0对x∈[0,2]恒成立,
则φ(x)=x+k+
在[0,2]递增,即h′(x)在[0,2]上为增函数,
∴h′(x)max=h′(2)=k+
,
∵h(x)在[0,2]上单调递减,
∴h′(x)≤0对x∈[0,2]恒成立,
即h′(x)max=k+
≤0,
∴k≤-
;
(Ⅲ)当x∈[0,
-1]时,g′(x)=ln(x+1)+1>0,
∴g(x)=(x+1)ln(x+1)在区间[0,
-1]上为增函数,
∴x∈[0,
-1]时,0≤g(x)≤
,
∵f(x)=
x2+kx+1的对称轴为x=-k,
∴为满足题意,必须-1<-k<4,
此时f(x)min=f(-k)=1-
k2,f(x)的值恒小于f(-1)和f(4)中最大的一个,
∵对于?t∈[0,
-1],总存在x1,x2∈(-1,4),且x1≠x2满足f(xi)=g(t)(i=1,2),
∴[0,
]⊆(f(x)min,min{f(-1),f(4)}),
∴
⇒
,
∴
-
<k<-
.
g′(x)=ln(x+1)+1,
则g(0)=0,g′(0)=1,
∴切线l:y=x,
由
|
∵l与函数f(x)的图象相切,
∴△=4(k-1)2-8=0⇒k=1±
| 2 |
(Ⅱ)h(x)=
| 1 |
| 2 |
| 1 |
| x+1 |
令φ(x)=x+k+
| 1 |
| x+1 |
φ′(x)=1-
| 1 |
| (x+1)2 |
| x(x+2) |
| (x+1)2 |
则φ(x)=x+k+
| 1 |
| x+1 |
∴h′(x)max=h′(2)=k+
| 7 |
| 3 |
∵h(x)在[0,2]上单调递减,
∴h′(x)≤0对x∈[0,2]恒成立,
即h′(x)max=k+
| 7 |
| 3 |
∴k≤-
| 7 |
| 3 |
(Ⅲ)当x∈[0,
| e |
∴g(x)=(x+1)ln(x+1)在区间[0,
| e |
∴x∈[0,
| e |
| 1 |
| 2 |
| e |
∵f(x)=
| 1 |
| 2 |
∴为满足题意,必须-1<-k<4,
此时f(x)min=f(-k)=1-
| 1 |
| 2 |
∵对于?t∈[0,
| e |
∴[0,
| 1 |
| 2 |
| e |
∴
|
|
∴
| 1 |
| 8 |
| e |
| 9 |
| 4 |
| 2 |
点评:本题考查导数的运用:求切线方程和单调区间及极值、最值,同时考查任意存在问题注意转化为函数的值域的包含关系,考查运算能力,属于中档题和易错题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设复数z1,z2在复平面内对应的点关于虚轴对称,若z1=1-2i,则
的虚部为( )
| z2 |
| z1 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知集合M={x|
≥0},则∁RM=( )
| 1+x |
| 1-x |
| A、{x|-1<x<1} |
| B、{x|-1<x≤1} |
| C、{x|x<-1或x≥1} |
| D、{x|x≤-1或x≥1} |
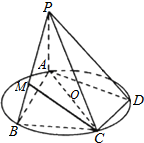 如图AC是圆O的直径,B、D是圆O上两点,AC=2BC=2CD=2,PA⊥圆O所在的平面,PA=
如图AC是圆O的直径,B、D是圆O上两点,AC=2BC=2CD=2,PA⊥圆O所在的平面,PA=