题目内容
正四棱锥的顶点都在同一球面上，若该棱锥的体积为
，底面边长为2，则该球的表面积为 ．
| 16 |
| 3 |
考点：球的体积和表面积
专题：计算题,空间位置关系与距离
分析：正四棱锥P-ABCD的外接球的球心在它的高PE上，求出球的半径，求出球的表面积．
解答：
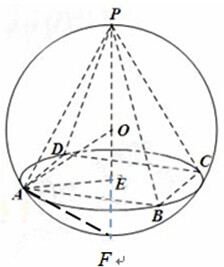解：如图，正四棱锥P-ABCD中，PE为正四棱锥的高，根据球的相关知识可知，正四棱锥的外接球的球心O必在正四棱锥的高线PE所在的直线上，
延长PE交球面于一点F，连接AE，AF，
棱锥的体积为
，底面边长为2，则棱锥的高为4，
由球的性质可知△PAF为直角三角形且AE⊥PF，根据平面几何中的射影定理可得PA2=PF•PE，因为AE=
=
，
所以侧棱长PA=
=3
，PF=2R，
所以18=2R×4，所以R=
，
所以S=4πR2=
．
故答案为：
．
解：如图，正四棱锥P-ABCD中，PE为正四棱锥的高，根据球的相关知识可知，正四棱锥的外接球的球心O必在正四棱锥的高线PE所在的直线上，延长PE交球面于一点F，连接AE，AF，
棱锥的体积为
| 16 |
| 3 |
由球的性质可知△PAF为直角三角形且AE⊥PF，根据平面几何中的射影定理可得PA2=PF•PE，因为AE=
| ||
| 2 |
| 2 |
所以侧棱长PA=
| 42+2 |
| 2 |
所以18=2R×4，所以R=
| 9 |
| 4 |
所以S=4πR2=
| 81π |
| 4 |
故答案为：
| 81π |
| 4 |
点评：本题考查球的表面积，球的内接几何体问题，考查计算能力，是基础题．
练习册系列答案
相关题目
在区间[-3，2]上随机选取一个数x，使得函数y=
有意义的概率为（ ）
| x+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设集合A={y|y=lnx，x＞1}，集合B={x|y=
}，则A∩∁RB=（ ）
| 4-x2 |
| A、∅ |
| B、（0，2] |
| C、（2，+∞） |
| D、（-∞，-2）∪（2，+∞） |
已知集合M={x|
≥0}，则∁RM=（ ）
| 1+x |
| 1-x |
| A、{x|-1＜x＜1} |
| B、{x|-1＜x≤1} |
| C、{x|x＜-1或x≥1} |
| D、{x|x≤-1或x≥1} |