题目内容
已知函数f(x)=loga(ax-1)(a>0,且a≠1)
(1)证明函数f(x)的图象在y轴的一侧
(2)设A(x1,y1),B(x2,y 2)(x1<x2)图象上两点,证明直线AB的斜率大于0.
(1)证明函数f(x)的图象在y轴的一侧
(2)设A(x1,y1),B(x2,y 2)(x1<x2)图象上两点,证明直线AB的斜率大于0.
考点:函数与方程的综合运用
专题:函数的性质及应用
分析:(1)由ax-1>0得:ax>1,a>1时,函数f(x)的图象在y轴的右侧;当0<a<1时,x<0,函数f(x)的图象在y轴的左侧.所以函数f(x)的图象在y轴的一侧.
(2)由于x1<x2,则直线AB的斜率k=
,y1-y2=loga(ax1-1)-loga(ax2-1)=loga
,再分a>1和0<a<1两种情况分别进行讨论.
(2)由于x1<x2,则直线AB的斜率k=
| y1-y2 |
| x1-x2 |
| ax1-1 |
| ax2-1 |
解答:
证明:(1)由ax-1>0得:ax>1,
当a>1时,x>0,即函数f(x)的定义域为(0,+∞),
此时函数f(x)的图象在y轴的右侧;
当0<a<1时,x<0,即函数f(x)的定义域为(-∞,0),
此时函数f(x)的图象在y轴的左侧.
所以函数f(x)的图象在y轴的一侧;
(2)由已知,直线AB的斜率k=
,
y1-y2=loga(ax1-1)-loga(ax2-1)=loga
,
下面分a>1和0<a<1两种情况分别进行讨论:
①当a>1时,由(1)知0<x1<x2,
∴1<ax1<ax2,
∴0<ax1-1<ax2-1,
∴0<
<1,
∴y1-y2<0,
又x1-x2<0,
从而斜率k>0;
②当0<a<1时,由(1)知x1<x2<0,
∴ax1>ax2>1,
∴ax1-1>ax2-1>0,
∴
>1,
∴y1-y2<0,
又x1-x2<0,
从而斜率k>0.
所以函数f(x)图象上任意两点连线的斜率都大于0.
当a>1时,x>0,即函数f(x)的定义域为(0,+∞),
此时函数f(x)的图象在y轴的右侧;
当0<a<1时,x<0,即函数f(x)的定义域为(-∞,0),
此时函数f(x)的图象在y轴的左侧.
所以函数f(x)的图象在y轴的一侧;
(2)由已知,直线AB的斜率k=
| y1-y2 |
| x1-x2 |
y1-y2=loga(ax1-1)-loga(ax2-1)=loga
| ax1-1 |
| ax2-1 |
下面分a>1和0<a<1两种情况分别进行讨论:
①当a>1时,由(1)知0<x1<x2,
∴1<ax1<ax2,
∴0<ax1-1<ax2-1,
∴0<
| ax1-1 |
| ax2-1 |
∴y1-y2<0,
又x1-x2<0,
从而斜率k>0;
②当0<a<1时,由(1)知x1<x2<0,
∴ax1>ax2>1,
∴ax1-1>ax2-1>0,
∴
| ax1-1 |
| ax2-1 |
∴y1-y2<0,
又x1-x2<0,
从而斜率k>0.
所以函数f(x)图象上任意两点连线的斜率都大于0.
点评:本题考查对数函数的性质和综合应用,解题时注意分类讨论思想的合理应用.

练习册系列答案
相关题目
已知集合M={x|
≥0},则∁RM=( )
| 1+x |
| 1-x |
| A、{x|-1<x<1} |
| B、{x|-1<x≤1} |
| C、{x|x<-1或x≥1} |
| D、{x|x≤-1或x≥1} |
函数f(x)=log2(x+1)+2的零点所在区间是( )
A、(-
| ||||
B、(
| ||||
C、(-1,
| ||||
D、(1,
|
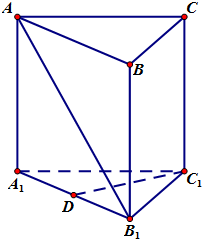 如图,直三棱柱ABC-A1B1C1中,AC=BC=
如图,直三棱柱ABC-A1B1C1中,AC=BC=