题目内容
已知α=-1910°．
（1）把角α写成β+k•360°（k∈Z，0°≤β＜360°）的形式，指出它是第几象限的角；
（2）求出θ的值，使θ与α的终边相同，且-720°≤θ＜0°．
（1）把角α写成β+k•360°（k∈Z，0°≤β＜360°）的形式，指出它是第几象限的角；
（2）求出θ的值，使θ与α的终边相同，且-720°≤θ＜0°．
考点：终边相同的角
专题：三角函数的求值
分析：（1）利用终边相同的假的表示方法，把角α写成β+k•360°（k∈Z，0°≤β＜360°）的形式，然后指出它是第几象限的角；
（2）利用终边相同的角的表示方法，通过k的取值，求出θ，且-720°≤θ＜0°．
（2）利用终边相同的角的表示方法，通过k的取值，求出θ，且-720°≤θ＜0°．
解答：
解：（1）∵-1910°=-6×360°+250°，180°＜250°＜270°，
∴把角α写成β+k•360°（k∈Z，0°≤β＜360°）的形式为：-1910°=-6×360°+25°，
它是第三象限的角．
（2）∵θ与α的终边相同，
∴令θ=k•360°+250°，k∈Z，
k=-1，k=-2满足题意，
得到θ=-110°，-470°．
∴把角α写成β+k•360°（k∈Z，0°≤β＜360°）的形式为：-1910°=-6×360°+25°，
它是第三象限的角．
（2）∵θ与α的终边相同，
∴令θ=k•360°+250°，k∈Z，
k=-1，k=-2满足题意，
得到θ=-110°，-470°．
点评：本题考查终边相同角的表示方法，基本知识的考查．
练习册系列答案
相关题目
已知函数f（x）=cosxsin2x，下列结论中不正确的是（ ）
| A、y=f（x）的图象关于（π，0）中心对称 | ||||
B、y=f（x）的图象关于x=
| ||||
C、f（x）的最大值为
| ||||
| D、f（x）既是奇函数，又是周期函数 |
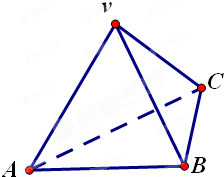如图，在三棱锥V-ABC中，VA=VB=AC=BC=2，AB=2