题目内容
已知函数f(x)=cosxsin2x,下列结论中不正确的是( )
| A、y=f(x)的图象关于(π,0)中心对称 | ||||
B、y=f(x)的图象关于x=
| ||||
C、f(x)的最大值为
| ||||
| D、f(x)既是奇函数,又是周期函数 |
考点:二倍角的正弦,二倍角的余弦
专题:三角函数的图像与性质
分析:利用二倍角公式与三角函数间的关系可将函数f(x)=cosxsin2x转化为f(x)=2sinx-2sin3x,再对A、B、C、D四个选项逐一分析即可.
解答:
解:f(x)=cosxsin2x=2sinxcos2x=2sinx(1-sin2x)=2sinx-2sin3x,
对于A:∵f(π-x)+f(π+x)=(2sinx-2sin3x)-(2sinx-2sin3x)=0,
∴y=f(x)的图象关于(π,0)中心对称,即A正确;
对于B:∵f(π-x)=2sinx-2sin3x=f(x),∴y=f(x)的图象关于x=
对称,即B正确;
对于C:y′=-sinxsin2x+2cosxcos2x
=-2sin2xcosx+2cosx(1-2sin2x)
=-6sin2xcosx+2cosx,
令y′=0得:(3sin2x-1)cosx=0,
∴当sinx=
时取得最大值
,故C错误;
对于D:∵f(-x)=f(x),∴是奇函数,又f(x+2π)=f(x),故是周期为2π的周期函数,故D正确;
故选:C.
对于A:∵f(π-x)+f(π+x)=(2sinx-2sin3x)-(2sinx-2sin3x)=0,
∴y=f(x)的图象关于(π,0)中心对称,即A正确;
对于B:∵f(π-x)=2sinx-2sin3x=f(x),∴y=f(x)的图象关于x=
| π |
| 2 |
对于C:y′=-sinxsin2x+2cosxcos2x
=-2sin2xcosx+2cosx(1-2sin2x)
=-6sin2xcosx+2cosx,
令y′=0得:(3sin2x-1)cosx=0,
∴当sinx=
| ||
| 3 |
4
| ||
| 9 |
对于D:∵f(-x)=f(x),∴是奇函数,又f(x+2π)=f(x),故是周期为2π的周期函数,故D正确;
故选:C.
点评:本题考查二倍角公式与三角函数间的关系,着重考查三角函数的周期性、对称性、奇偶性及最值的综合应用,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列命题中,是假命题的是( )
| A、给定(ρ,θ),在极坐标系中有惟一确定的点M与之相对应 |
| B、给定平面内任意一点M,有惟一的极坐标(ρ,θ)与之相对应 |
| C、给定实数对(x,y)在平面直角坐标系中有惟一确定的点M与之相对应 |
| D、给定平面直角坐标系中任一点M有惟一一组实数对(x,y)与之相对应 |
等差数列{an}中,S10=120,那么a5+a6的值是( )
| A、12 | B、24 | C、36 | D、48 |
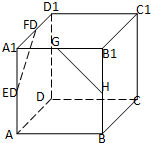 如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别是AA1,A1D1,A1B1,BB1的中点,则异面直线EF与GH所成的角的大小为( )
如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别是AA1,A1D1,A1B1,BB1的中点,则异面直线EF与GH所成的角的大小为( )| A、30° | B、45° |
| C、60° | D、120° |
用1,2,3,4这四个数字可排成必须含有重复数字的四位数有( )
| A、265个 | B、232个 |
| C、128个 | D、24个 |