题目内容
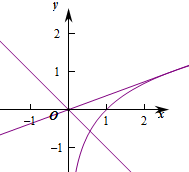
已知直线y=kx与曲线y=lnx有公共点,则k的最大值为 .
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:根据导数的几何意义,即可求出k的最大值.
解答:
 解:若k≤0,则满足条件,
解:若k≤0,则满足条件,
当k>0,直线y=kx与y=lnx相切时,此时k取得最大值.
设切点为(a,b),
则函数的导数为f′(x)=
,
即切线斜率k=f′(a)=
,
则切线方程为y-b=
(x-a)=
x-1,
即y=
x+b-1=
x+lna-1,
∵y=kx是切线,
∴
,解得a=e,k=
,
若直线y=kx与曲线y=lnx有公共点,
则k≤
,
即k的最大值为
,
故答案为:
 解:若k≤0,则满足条件,
解:若k≤0,则满足条件,当k>0,直线y=kx与y=lnx相切时,此时k取得最大值.
设切点为(a,b),
则函数的导数为f′(x)=
| 1 |
| x |
即切线斜率k=f′(a)=
| 1 |
| a |
则切线方程为y-b=
| 1 |
| a |
| 1 |
| a |
即y=
| 1 |
| a |
| 1 |
| a |
∵y=kx是切线,
∴
|
| 1 |
| e |
若直线y=kx与曲线y=lnx有公共点,
则k≤
| 1 |
| e |
即k的最大值为
| 1 |
| e |
故答案为:
| 1 |
| e |
点评:本题主要考查方程交点的应用,根据导数的几何意义转化为求函数的切线斜率是解决本题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
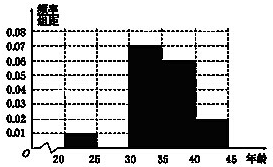 对某项活动中800名青年志愿者的年龄抽样调查后,得到如图所示的频率分布直方图,但年龄在25,30)的数据不慎丢失.依据此图,估计该项活动中年龄在25,30)的志愿者人数为
对某项活动中800名青年志愿者的年龄抽样调查后,得到如图所示的频率分布直方图,但年龄在25,30)的数据不慎丢失.依据此图,估计该项活动中年龄在25,30)的志愿者人数为