题目内容
8.下列函数中,既是偶函数又在区间(0,1)内单调递减的是( )| A. | y=x3 | B. | y=2|x| | C. | y=cosx | D. | $y=lnx-\frac{1}{x}$ |
分析 根据函数奇偶性和单调性的性质进行判断即可.
解答 解:A.y=x3是奇函数,在区间(0,1)内单调递增,不满足条件.
B.y=2|x|是偶函数,在区间(0,1)内单调递增,不满足条件.
C.y=cosx是偶函数,在区间(0,1)内单调递减,满足条件.
D.$y=lnx-\frac{1}{x}$lnx是非奇非偶函数,在区间(0,1)内单调递增,不满足条件.
故选:C.
点评 本题主要考查函数奇偶性和单调性的判断,要求熟练掌握常见函数的奇偶性和单调性的性质.

练习册系列答案
相关题目
18.命题“|x|+|y|≠0”是命题“x≠0或y≠0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
16.已知函数f(x)=$\frac{x}{{e}^{x}}$,则f′(x)=( )
| A. | $\frac{x-1}{{e}^{x}}$ | B. | $\frac{x+1}{{e}^{x}}$ | C. | $\frac{-x-1}{{e}^{x}}$ | D. | $\frac{1-x}{{e}^{x}}$ |
20.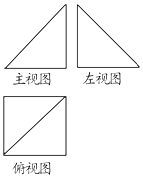 如图,已知某几何体的主视图和左视图是全等的等腰直角三角形,俯视图是边长为2的正方形,那么它的体积是( )
如图,已知某几何体的主视图和左视图是全等的等腰直角三角形,俯视图是边长为2的正方形,那么它的体积是( )
 如图,已知某几何体的主视图和左视图是全等的等腰直角三角形,俯视图是边长为2的正方形,那么它的体积是( )
如图,已知某几何体的主视图和左视图是全等的等腰直角三角形,俯视图是边长为2的正方形,那么它的体积是( )| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | 4 | D. | $\frac{16}{3}$ |
17.已知抛物线C:x2=2y的焦点为F,A(x0,y0)是C上一点,|AF|=$\frac{5}{4}{y_0}$,则x0=( )
| A. | 1 | B. | -1或1 | C. | 2 | D. | -2或2 |
8.已知$\overrightarrow{AB}$=(cos23°,cos67°),$\overrightarrow{BC}$=(2cos68°,2cos22°),则△ABC的面积为( )
| A. | 2 | B. | $\sqrt{2}$ | C. | 1 | D. | $\frac{\sqrt{2}}{2}$ |
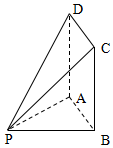 如图,四边形ABCD为矩形,PB=20,BC=30,PA⊥平面ABCD.
如图,四边形ABCD为矩形,PB=20,BC=30,PA⊥平面ABCD.