题目内容

17．已知抛物线C：x2=2y的焦点为F，A（x0，y0）是C上一点，|AF|=$\frac{5}{4}{y_0}$，则x0=（　　）
A．1B．-1或1C．2D．-2或2

分析 求出抛物线的焦点坐标，利用A（x0，y0）是C上一点，|AF|=$\frac{5}{4}{y_0}$，列出方程化简求解即可．

解答 解：抛物线C：x2=2y的焦点为F（0，$\frac{1}{2}$），A（x0，y0）是C上一点，|AF|=$\frac{5}{4}{y_0}$，
可得：$\sqrt{（{x}_{0}-0）^{2}+（{y}_{0}-\frac{1}{2}）^{2}}$=$\frac{5}{4}{y}_{0}$，
可得${{x}_{0}}^{2}$+${{y}_{0}}^{2}$-y0+$\frac{1}{4}$=$\frac{25}{16}{{y}_{0}}^{2}$，
即${{y}_{0}}^{2}$+y0+$\frac{1}{4}$=$\frac{25}{16}{{y}_{0}}^{2}$，解得y0=2，
可得x0=±2．
故选：D．

点评 本题考查抛物线的简单性质的应用，考查转化思想以及计算能力．

练习册系列答案
相关题目
7．已知函数f（x）=ax3+bx+12在x=2处取得极值为-4．
（1）求a、b的值；
（2）求f（x）在[-3，3]上的最大值．
8．下列函数中，既是偶函数又在区间（0，1）内单调递减的是（　　）
A．y=x3B．y=2|x|C．y=cosxD．$y=lnx-\frac{1}{x}$
5．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0\;，b＞0}）$的一条渐近线过点（2，2），则双曲线的离心率等于$\sqrt{2}$．
12．若曲线Cl：x2+y2-2x=0与曲线C2：（x-1）（y-mx-m）=0有四个不同的交点，则实数m的取值范围是（　　）
A．$（{-\frac{{\sqrt{3}}}{3}，\frac{{\sqrt{3}}}{3}}）$B．$（{-\frac{{\sqrt{3}}}{3}，0}）∪（{0，\frac{{\sqrt{3}}}{3}}）$C．$[{-\frac{{\sqrt{3}}}{3}，\frac{{\sqrt{3}}}{3}}]$D．$（{-∞，-\frac{{\sqrt{3}}}{3}}）∪（{\frac{{\sqrt{3}}}{3}，+∞}）$
2．已知向量$\overrightarrow a$，$\overrightarrow b$夹角为$\frac{3π}{4}$，且$\overrightarrow a=（1，1）$，$|{\overrightarrow a-2\overrightarrow b}|=\sqrt{10}$，则|$\overrightarrow b$|=2．
9．已知函数f（x）=ax+lnx-1，其中a为常数
（1）当$a∈（-∞，-\frac{1}{e}）$时，若f（x）在区间（0，e）上的最大值为-3，求a的值；
（2）当$a=-\frac{1}{e}$时，若$g（x）=|{f（x）}|-\frac{lnx}{x}-\frac{b}{2}$存在零点，求实数b的取值范围．
16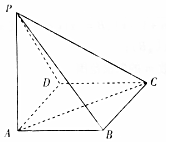．如图，在底面为正方形的四棱锥P-ABCD中，侧面PAD⊥底面ABCD，PA⊥AD，PA=AD，则异面直线PB与AC所成的角为（　　）
A．30°B．45°C．60°D．90°
17．与双曲线2x2-y2=3有相同渐近线，且过点P（1，2）的双曲线的方程为（　　）
A．2x2-$\frac{{y}^{2}}{4}$=1B．$\frac{{y}^{2}}{2}$-x2=1C．x2-$\frac{{y}^{2}}{2}$=1D．$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{4}$=1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网