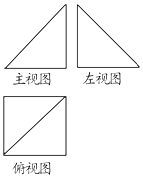如图.已知某几何体的主视图和左视图是全等的等腰直角三角形.俯视图是边长为2的正方形.那么它的体积是( )A．$\frac{4}{3}$B．$\frac{8}{3}$C．4D．$\frac{16}{3}$ 题目和参考答案——青夏教育精英家教网—

题目内容

20．

如图，已知某几何体的主视图和左视图是全等的等腰直角三角形，俯视图是边长为2的正方形，那么它的体积是（　　）

A．

$\frac{4}{3}$

B．

$\frac{8}{3}$

C．

D．

$\frac{16}{3}$

分析已知中的三视图，可得：该几何体是一个以俯视图为底面的四棱锥，代入锥体体积和表面积公式，可得答案．

解答解：由已知中的三视图，可得：该几何体是一个以俯视图为底面的四棱锥，
其底面的面积S=2×2=4，
高h=2，
故三棱锥的体积V=$\frac{1}{3}Sh$=$\frac{8}{3}$，
故选：B

点评本题考查的知识点是棱柱的体积和表面积，棱锥的体积和表面积，简单几何体的三视图，难度基础．

练习册系列答案

黄冈经典阅读系列答案

文言文课外阅读特训系列答案

轻松阅读训练系列答案

南大教辅初中英语任务型阅读与首字母填空系列答案

相关题目

10．已知命题p：任意x∈R，sinx≤1，则（　　）

	A．	￢p：存在x∈R，sinx≥1		B．	￢p：任意x∈R，sinx≥1
	C．	￢p：存在x∈R，sinx＞1		D．	￢p：任意x∈R，sinx＞1

11．已知数列{a_n}的前n项和S_n=n²-n（n∈N*）．正项等比数列{b_n}的首项b₁=1，且3a₂是b₂，b₃的等差中项．
（I）求数列{a_n}，{b_n}的通项公式；
（II）若c_n=$\frac{{a}_{n}}{{b}_{n}}$，求数列{c_n}的前n项和T_n．

8．下列函数中，既是偶函数又在区间（0，1）内单调递减的是（　　）

15．设S_n为等差数列{a_n}的前n项和，若a₁=1，S₇-S₅=24，则S₆=36．

5．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0\;，b＞0}）$的一条渐近线过点（2，2），则双曲线的离心率等于$\sqrt{2}$．

12．若曲线C_l：x²+y²-2x=0与曲线C₂：（x-1）（y-mx-m）=0有四个不同的交点，则实数m的取值范围是（　　）

A．

$（{-\frac{{\sqrt{3}}}{3}，\frac{{\sqrt{3}}}{3}}）$

B．

$（{-\frac{{\sqrt{3}}}{3}，0}）∪（{0，\frac{{\sqrt{3}}}{3}}）$

C．

$[{-\frac{{\sqrt{3}}}{3}，\frac{{\sqrt{3}}}{3}}]$

D．

$（{-∞，-\frac{{\sqrt{3}}}{3}}）∪（{\frac{{\sqrt{3}}}{3}，+∞}）$

9．已知函数f（x）=ax+lnx-1，其中a为常数
（1）当$a∈（-∞，-\frac{1}{e}）$时，若f（x）在区间（0，e）上的最大值为-3，求a的值；
（2）当$a=-\frac{1}{e}$时，若$g（x）=|{f（x）}|-\frac{lnx}{x}-\frac{b}{2}$存在零点，求实数b的取值范围．

20．函数f（x）=-x³+3x²+9x+a，x∈[-2，2]的最小值为-2，则f（x）的最大值为（　　）

试题分类