题目内容
19.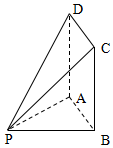 如图,四边形ABCD为矩形,PB=20,BC=30,PA⊥平面ABCD.
如图,四边形ABCD为矩形,PB=20,BC=30,PA⊥平面ABCD.(1)证明:平面PCD⊥平面PAD;
(2)当AB的长为多少时,面PAB与面PCD所成的二面角为60°?请说明理由.
分析 (1)推导出AB⊥AD,PA⊥AB,从而AB⊥平面PAD,再由AB∥CD,能证明平面PCD⊥平面PAD.
(2)以A为原点,AP,AB,AD所以直线分别为x轴,y轴,z轴建立空间直角坐标系,利用向量法能求出当AB的长为1时,面PAB与面PCD所成的二面角为60°.
解答 (本小题满分12分)
证明:(1)∵四边形为矩形,∴AB⊥AD,
∵PA⊥平面ABCD,∴PA⊥AB,且PA∩AD=A,
∴AB⊥平面PAD,
∵四边形ABCD为矩形,∴AB∥CD,
∴CD⊥平面PAD,
又因为CD?平面PCD,
∴平面PCD⊥平面PAD.…(6分)
解:(2)如图,以A为原点,AP,AB,AD所以直线分别为x轴,y轴,z轴建立空间直角坐标系,
设AB=a,则A(0,0,0),P($\sqrt{4-{a}^{2}}$,0,0),B(0,a,0),C(0,a,3),D(0,0,3)
$\overrightarrow{PC}$=(-$\sqrt{4-{a}^{2}}$,a,3),$\overrightarrow{PD}$=(-$\sqrt{4-{a}^{2}}$,0,3),
设平面PCD的法向量为$\overrightarrow{n}$=(x,y,z),则由$\overrightarrow{PC}$⊥$\overrightarrow{n}$,$\overrightarrow{PD}$⊥$\overrightarrow{n}$得:
-$\sqrt{4-{a}^{2}}$•x+ay+3z=0,-$\sqrt{4-{a}^{2}}$x+3z=0
∴$\overrightarrow{n}$=(3,0,-$\sqrt{4-{a}^{2}}$)
平面PAB的法向量为$\overrightarrow{m}$=(0,0,1)
又面PAB与面PCD所成的二面角为锐二面角,面PAB与面PCD所成的二面角为60°,
∴cos60°=$\frac{|\overrightarrow{n}•\overrightarrow{m}|}{|\overrightarrow{n}|•|\overrightarrow{m}|}$=$\frac{\sqrt{4-{a}^{2}}}{\sqrt{13-{a}^{2}}}$,即:$\sqrt{13-{a}^{2}}$=2$\sqrt{4-{a}^{2}}$,
解得a=1
∴当AB的长为1时,面PAB与面PCD所成的二面角为60°.…(12分)
点评 本题考查面面垂直的证明,考查满足二面角为60°的线段长的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

| A. | 3 | B. | $\sqrt{3}$ | C. | -3 | D. | -$\sqrt{3}$ |
| A. | ¬p:存在x∈R,sinx≥1 | B. | ¬p:任意x∈R,sinx≥1 | ||
| C. | ¬p:存在x∈R,sinx>1 | D. | ¬p:任意x∈R,sinx>1 |
| A. | y=x3 | B. | y=2|x| | C. | y=cosx | D. | $y=lnx-\frac{1}{x}$ |