题目内容
8.已知$\overrightarrow{AB}$=(cos23°,cos67°),$\overrightarrow{BC}$=(2cos68°,2cos22°),则△ABC的面积为( )| A. | 2 | B. | $\sqrt{2}$ | C. | 1 | D. | $\frac{\sqrt{2}}{2}$ |
分析 根据题意,利用$\overrightarrow{BA}$,$\overrightarrow{BC}$的坐标,可得$\overrightarrow{BA}$,$\overrightarrow{BC}$的模,由数量积公式,可得$\overrightarrow{BA}•\overrightarrow{BC}$的值,进而由cos∠B=$\frac{\overrightarrow{BA}•\overrightarrow{BC}}{|\overrightarrow{BA}||\overrightarrow{BC}|}$,可得cos∠B,由余弦函数的性质,可得∠B,最后由三角形面积公式,计算可得答案.
解答 解:根据题意,$\overrightarrow{AB}$=(cos23°,cos67°),则$\overrightarrow{BA}$=-(cos23°,sin23°),有|$\overrightarrow{BA}$|=1,
由于,$\overrightarrow{BC}$=(2cos68°,2cos22°)=2(cos68°,sin68°),则|$\overrightarrow{BC}$|=2,
则$\overrightarrow{BA}•\overrightarrow{BC}$=-2(cos23°cos68°+sin23°sin68°)=-2×cos45°=-$\sqrt{2}$,
可得:cos∠B=$\frac{\overrightarrow{BA}•\overrightarrow{BC}}{|\overrightarrow{BA}||\overrightarrow{BC}|}$=-$\frac{\sqrt{2}}{2}$,
则∠B=135°,
则S△ABC=$\frac{1}{2}$|$\overrightarrow{BA}$|•|$\overrightarrow{BC}$|sin∠B=$\frac{1}{2}×1×2×\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{2}$;
故选:D.
点评 本题考查数量积的坐标运算,关键是由余弦函数的和角公式求出$\overrightarrow{BA}$•$\overrightarrow{BC}$,注意角B是向量$\overrightarrow{BA}$、$\overrightarrow{BC}$的夹角,属于中档题.

| A. | y=x3 | B. | y=2|x| | C. | y=cosx | D. | $y=lnx-\frac{1}{x}$ |
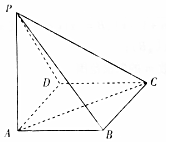 如图,在底面为正方形的四棱锥P-ABCD中,侧面PAD⊥底面ABCD,PA⊥AD,PA=AD,则异面直线PB与AC所成的角为( )
如图,在底面为正方形的四棱锥P-ABCD中,侧面PAD⊥底面ABCD,PA⊥AD,PA=AD,则异面直线PB与AC所成的角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
| A. | 672 | B. | 673 | C. | 3024 | D. | 1345 |
| A. | 25 | B. | 23 | C. | 21 | D. | 20 |
| A. | 2x2-$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{y}^{2}}{2}$-x2=1 | C. | x2-$\frac{{y}^{2}}{2}$=1 | D. | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{4}$=1 |
| 次数 | 1 | 2 | 3 | 4 |
| 人数 | 1 | 4 | 4 | 1 |
(Ⅰ)设A为事件“选出的2人参加义工活动次数之和为6”,求事件A发生的概率;
(Ⅱ)设X为选出的2人参加义工活动次数之和,求随机变量X的分布列和数学期望.