题目内容
若x∈（2，4），则下列结论正确的是（ ）
| A、2x＞x2＞log2x |
| B、x2＞log2x＞2x |
| C、log2x＞x2＞2x |
| D、x2＞2x＞log2x |
考点：不等式比较大小
专题：函数的性质及应用
分析：如图所示，当x∈（2，4），x2＞2x＞4．而log2x＜2．即可得出．
解答：
解：如图所示，
当x∈（2，4），x2＞2x＞4．
而log2x＜2．
综上可得：x2＞2x＞log2x．
故选：D．
当x∈（2，4），x2＞2x＞4．
而log2x＜2．
综上可得：x2＞2x＞log2x．
故选：D．
点评：本题考查了指数函数、幂函数、对数函数的单调性，考查了数形结合的思想方法，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
给定函数①y=x，②y=log
（x+1），③y=|x-1|，④y=2x+1，其中在区间（0，1）上单调递减的函数的序号是（ ）
| 1 |
| 2 |
| A、①② | B、②③ | C、③④ | D、①④ |
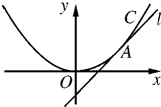如图，直线l：y=x+b与抛物线C：x2=4y相切于点A．